A note from Andy Pepperdine of Bath informed me that \(2^2 + 3^3 +5^5 + 7^7 = 826699 \), a prime.
The sum of the first eight digits of pi = 3+1+4+1+5+9+2+6 = 31. *Prime Curios
There are only 31 numbers that cannot be expressed as the sum of distinct squares. *Prime curios
31 is the number of regular polygons with an odd number of sides that are known to be constructible with compass and straightedge.
The numbers 31, 331, 3331, 33331, 333331, 3333331, and 33333331 are all prime. For a time it was thought that every number of the form 3w1 would be prime. However, the next nine numbers of the sequence are composite *Wik
31 = 5^0 + 5^1 + 5^2 and also 31 = 2^0 + 2^1 + 2^2 + 2^3 + 2^4. *Mario Livio says that there are only two known numbers that can be expressed as consecutive powers of a number in two different ways. The second is 8191, which can be expressed as consecutive powers of two, and of ninety.
\(\pi^3\) (almost)=31 (31,006...)
There are only 31 numbers that cannot be expressed as the sum of distinct squares.
31 is the minimum number of moves to solve the Towers of Hanoi problem. The general solution for any number of discs is a Mersenne number of the form 2^n -1.
Jim Wilder @wilderlab offered, The sum of digits of the 31st Fibonacci number (1346269) is 31.
If you like unusual speed limits, the speed limit in downtown Trenton, a small city in northwestern Tennessee, is 31 miles per hour. And the little teapot on the sign? Well, Trenton also bills itself as the teapot capital of the nation. The 31 mph road sign seems to come from a conflict between Trenton and a neighboring town which I will not name ,...but I will tell you they think of themselves as the white squirrel capital.
31 is also the smallest integer that can be written as the sum of four positive squares in two ways 1+1+4+25; 4+9+9+9.
31 is an evil math teacher number. The sequence of the maximum number of regions obtained by joining n points around a circle by straight lines begins 2, 4, 8, 16... but for five points, it is 31.
@JamesTanton posted a mathematical fact and query regarding 31. 31 =111(base 5) =11111(base 2) and 8191 =111(base 90) = 111111111111(base 2) are the only two integers known to be repunits at least 3 digits long in two different bases. Is there an integer with representations 10101010..., ,at least three digits, in each of two different bases? Which made me wonder, are there other pairs that are repdigits (all alike, but not all units) in two (or more) different bases?
The 32nd day of the year; 32 is conjectured to be the highest power of two with all prime digits. *Number Gossip (Could 27 hold the similar property for powers of three?)
Also, 131 is the 32nd prime and the sum of the digits of both numbers is 5. 32 & 131 is the smallest n, P(n) with this property. \( 32 = 1^1 + 2^2 + 3^3 \)
A fermat prime is a prime number of the form \(2^{2^n} +1 \) and five are known (3, 5, 17, 257, 65537). Their product is \( 2^{32} -1\)
32! - 1 and 33!-1 are both primes
[David Marain pointed out that the products of the first n are all expressible in 2n-1 form, \( 3x5 = 2^4-1, 3x5x17 = 2^8-1\), and \(3x5x7x257 = 2^{16}-1 \) ]
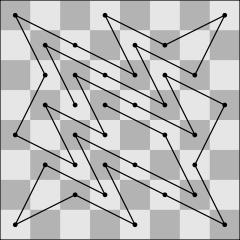
On an 8x8 chessboard, the longest closed non-crossing knight's path is 32 moves.
The integers 1 through n=32 can be arranged in a circle so that every adjacent pair sums to a perfect square. (Try it!)
Can those numbers be arranged in a circle such that any THREE adjacent numbers sum to a perfect square? *HT Matt Enlow
The 33rd Day of the Year;
among the infinity of integers, there are only six that can not be formed by the addition of distinct triangular numbers. The largest of these is 33. What are the other five?
33 = 1!+2!+3!+4! *jim wilder @wilderlab
33 is the smallest n such that n, n+1 and n+2 are all semi-primes, the products of two primes. *Bob S McDonald
32! - 1 and 33!-1 are both primes
The 33 letter Dutch word nepparterrestaalplaatserretrappen is the longest palindrome I know in any language. It means fake stairways from the ground floor to the sun lounge, made of steel plate. The shorter word "saippuakauppias" for a soap vendor is the longest single word palindrome in the world that is in everyday use. *Wiktionary
1033 is the largest known power of ten that can be expressed as the power of two factors neither of which contains a zero. 1033 = 233 533 = 8,589,934,592 x 116,415,321,826,934,814,453,125 *Cliff Pickover @pickover
The smallest odd number n such that n+x! is not a prime, for any number x.
33 is the smallest teo-digit palindrome in base ten which is also a palindrome in a smaller base.
The 34th day of the year; 34 is the smallest integer such that it and both its neighbors are the product of the same number of primes.
The concatenation of 34 and 35 has a unique property known only two two numbers, raising each digit to the power of itself and summing gives the original number. 3^3 + 4^4 + 3^3 + 5^5 = 3435.
The 33rd Day of the Year;
among the infinity of integers, there are only six that can not be formed by the addition of distinct triangular numbers. The largest of these is 33. What are the other five?
33 = 1!+2!+3!+4! *jim wilder @wilderlab
33 is the smallest n such that n, n+1 and n+2 are all semi-primes, the products of two primes. *Bob S McDonald
32! - 1 and 33!-1 are both primes
The 33 letter Dutch word nepparterrestaalplaatserretrappen is the longest palindrome I know in any language. It means fake stairways from the ground floor to the sun lounge, made of steel plate. The shorter word "saippuakauppias" for a soap vendor is the longest single word palindrome in the world that is in everyday use. *Wiktionary
1033 is the largest known power of ten that can be expressed as the power of two factors neither of which contains a zero. 1033 = 233 533 = 8,589,934,592 x 116,415,321,826,934,814,453,125 *Cliff Pickover @pickover
The smallest odd number n such that n+x! is not a prime, for any number x.
33 is the smallest teo-digit palindrome in base ten which is also a palindrome in a smaller base.
The 34th day of the year; 34 is the smallest integer such that it and both its neighbors are the product of the same number of primes.
The concatenation of 34 and 35 has a unique property known only two two numbers, raising each digit to the power of itself and summing gives the original number. 3^3 + 4^4 + 3^3 + 5^5 = 3435.
The only other is 438,579,088. *Fermat's Library
34 is the smallest number which can be expressed as the sum of two primes in four ways.*Prime Curios
A 4x4 magic square using the integers 1 to 16 has a magic constant of 34. An early example is in the tenth century Parshvanath Jain temple in Khajuraho. The image below was taken by Debra Gross Aczel, the wife of the late Amir D. Aczel who used the image in his last book, Finding Zero.
4x4 magic squares were written about in India by a mathematician named Nagarjuna as early as the first century.
The 35th Day of The Year, There are 35 hexominos, the polyominoes made from 6 squares. *Number Gossip (I only recently learned that, Although a complete set of 35 hexominoes has a total of 210 squares, which offers several possible rectangular configurations, it is not possible to pack the hexominoies into a rectangle.)
Chaw wrote, "Re. the observation that "NERD" is prime in base 35: I think base 36 is a lot more natural than base 35, given the conventional 10 digits and 26 Latin letters, which makes the following more interesting: NERDIEST is prime in base 36."
The concatenation of 34 and 35, 3435, has a unique property known only two two numbers, raising each digit to the power of itself and summing gives the original number. 3^3 + 4^4 + 3^3 + 5^5 = 3435.
The only other is 438,579,088. *Fermat's Library
The 36th Day of the Year, The 36th day of the year; 36 is the smallest non trivial number which is both triangular and square. It's also the largest day number of the year which is both. What's the next? You can find an infinity of them using this beautiful formula from Euler, Hat Tip to Vincent PANTALONI @panlepan
The sum of the first 36 integers, \(\sum_{k=1}^{36} k = 666\) the so called "number of the beast." Notice that a \(6^2\) (a triangular number) consecutive integers forms a repdigit triangular number, 666.
36 itself is the last year day which is both a square and a triangular number. The next square that is a triangular number is 1225. (The square of 36-1)
36 is also the smallest triangular number that is the sum of two consecutive triangular numbers
And Mario Livio pointed out in a tweet that Feb 5 is 5/2 in European style dating, and 52 is the maximum number of moves needed to solve the "15" sliding puzzle from any solvable position.
The Kiwi's seeds divide the circle into 36 equal sections. Nature's protractor. *Matemolivares@Matemolivares
A special historical tribute to 36: The thirty-six officers problem is a mathematical puzzle proposed by Leonhard Euler in 1782. He asked if it were possible to place officers of six ranks from each of six regiments in a 6x6 square so that no row or column would have an officer of the same rank, or the same regiment. Euler suspected that it could not be done. Euler knew how to construct such squares for nxn when n was odd, or a multiple of four, and he believed that all such squares with n = 4m+2 (6, 10, 14...) were impossible ( Euler didn't say it couldn't be done. He just said that his method does not work for numbers of that form.) Proof that he was right for n=6 took a while. French mathematician (and obviously a very patient man) Gaston Tarry proved it in 1901 by the method of exhaustion. He wrote out each of the 9408 6x6 squares and found that none of them worked. Then in 1959, R.C. Bose and S. S. Shrikhande proved that all the others could be constructed. So the thirty-six square is the only one that can't be done.
Jim Wilder sent \(36^2 = 1296\) and 1 + 29 + 6 = 36
Chaw wrote, "Re. the observation that "NERD" is prime in base 35: I think base 36 is a lot more natural than base 35, given the conventional 10 digits and 26 Latin letters, which makes the following more interesting: NERDIEST is prime in base 36."
Touchard (1953) proved that an odd perfect number, if it exists, must be of the form 12k+1 or 36k+9 *Wolfram Mathworld
The Kiwi's seeds divide the circle into 36 equal sections. Nature's protractor. *Matemolivares@Matemolivares
A special historical tribute to 36: The thirty-six officers problem is a mathematical puzzle proposed by Leonhard Euler in 1782. He asked if it were possible to place officers of six ranks from each of six regiments in a 6x6 square so that no row or column would have an officer of the same rank, or the same regiment. Euler suspected that it could not be done. Euler knew how to construct such squares for nxn when n was odd, or a multiple of four, and he believed that all such squares with n = 4m+2 (6, 10, 14...) were impossible ( Euler didn't say it couldn't be done. He just said that his method does not work for numbers of that form.) Proof that he was right for n=6 took a while. French mathematician (and obviously a very patient man) Gaston Tarry proved it in 1901 by the method of exhaustion. He wrote out each of the 9408 6x6 squares and found that none of them worked. Then in 1959, R.C. Bose and S. S. Shrikhande proved that all the others could be constructed. So the thirty-six square is the only one that can't be done.
Jim Wilder sent \(36^2 = 1296\) and 1 + 29 + 6 = 36
Chaw wrote, "Re. the observation that "NERD" is prime in base 35: I think base 36 is a lot more natural than base 35, given the conventional 10 digits and 26 Latin letters, which makes the following more interesting: NERDIEST is prime in base 36."
Touchard (1953) proved that an odd perfect number, if it exists, must be of the form 12k+1 or 36k+9 *Wolfram Mathworld
36^4 = 1679616, and the sum of the digits is 36. It is the largest number for which the sum of the digits of n^4 is equal to n .There are three smaller numbers (Not counting 1) which have this property also.
and 36^5 = 60466176 which also has a sum of digits of 36. I haven't found any other numbers where sum of digits of N^a and N^b are the same.
The 37th Day of the Year.
The 37th day of the year; 37 is the only prime with a three digit period for the decimal expansion of its reciprocal, 1/37 = .027027.... But 37 has a strange affinity with 27, which also has a three digit period for its reciprocal, .037037..., The affinity, of course, is due to 27 x 37 = 999
Can we call numbers like this, amicable reciprocals?
and Alex Kontorovich found 1/1287 = .000777000777... and yeah, 1/777 = .001287001287... Now you can find some of your own (and make sure to send me a note)!
Speaking of prime periods, students should know that the longest repeating decimal for the inverse of a prime number p is p-1. It seems that about 37% of the primes reach this max, but not 37 as mentioned above.
and Alex Kontorovich found 1/1287 = .000777000777... and yeah, 1/777 = .001287001287... Now you can find some of your own (and make sure to send me a note)!
Speaking of prime periods, students should know that the longest repeating decimal for the inverse of a prime number p is p-1. It seems that about 37% of the primes reach this max, but not 37 as mentioned above.
Big Prime::: n = integer whose digits are (left to right) 6424 copies of 37, followed by units digit of 3, is prime (n = 3737...373 has 12849 digits) *Republic of Math
1 × 2 - 1 = 1 37 × 2 − 1 = 73 397 × 2 − 1 = 793 3997 × 2 − 1 = 7993 39997 × 2 − 1 = 79993 and so on... "1, 37, 397, 3997, 39997, ... are the only positive integers N whose digit reversal is equal to 2N − 1. I proved this seven years ago. :)" *David Radcliffe
An amazing reversal: 37 is the 12th prime; and 73 is the 21st prime . This enigma is the only known combination.
37 is the last year day such that the sum of the squares of the first n primes, is divisible by n. There are only three such numbers in the days of the year. Two of them are primes themselves.
If you use multiplication and division operations to combine Fibonacci numbers, (for example, 4 = 2^2, 6 = 2·3, 7 = 21/ 3 ,...) you can make almost any other number. Almost, but you can't make 37. In fact, there are 12 numbers less than 100 that can not be expressed as "Fibonacci Integers" *Carl Pomerance, et
37! + 1 is a prime. It is the sixth Year Day for which this is true, and the last prime year day. There are only 13 Year Days for which n! + 1 is prime.
A pretty observation from Cliff Pickover , What do you wonder??? Well, check! Like what happens with numbers beyond 9?
To represent every integer as a sum of fifth powers requires at most 37 integers.
The last odd Roman numeral alphabetically is XXXVII (37). *prime Curios
Can we call numbers like this, amicable reciprocals?
and Alex Kontorovich found 1/1287 = .000777000777... and yeah, 1/777 = .001287001287...
The 38th Day Of the Year , 31415926535897932384626433832795028841 is a prime number. BUT, It’s also the first 38 digits of pi.
38 is the largest even number so that every partition of it into two odd integers must contain a prime.
\(38^2\) is the smallest square that ends in three 4's, 1444.
38 is the largest even number that can only be expressed as the sum of two distinct primes in one way. (31 + 7)
38 is the sum of squares of the first three primes \(2^2 + 3^2 + 5^2 = 38 \). *Prime Curios
Although we've had some unusual shaped flags, usually the star field is in a rectangle with the stars displaying some kind of (generally rectangular) similarity. Some have strayed greatly from the rectangle form however. This one with 38 stars from 1877 until 1890 is an example.
At the beginning of the 21st Century there were 38 known Mersenne Primes. As of this writing, there are 51, the last being discovered in Dec of 2018..
38 is also the magic constant in the only possible magic Yhexagon which utilizes all the natural integers up to and including 19. It was discovered independently by Ernst von Haselberg in 1887, W. Radcliffe in 1895, and several others. Eventually it was also discovered by Clifford W. Adams, who worked on the problem from 1910 to 1957. He worked on the problem throughout his career as a freight-handler and clerk for the Reading Rail Road by trial and error and after many years arrived at the solution which he transmitted to Martin Gardner in 1963. Gardner sent Adams' magic hexagon to Charles W. Trigg, who by mathematical analysis found that it was unique disregarding rotations and reflections.
The 39th Day of the Year, 39 is the smallest number with multiplicative persistence 3. [Multiplicative persistence is the number of times the digits must be multiplied until they produce a one digit number; 3(9)= 27; 2(7) = 14; 1(4)=4. Students might try to find the smallest number with multiplicative persistence of four, or prove that no number has multiplicative persistence greater than 11]
39 = 3¹ + 3² + 3³ *jim wilder @wilderlab An Armstrong (or Pluperfect digital invariant) number is a number that is the sum of its own digits each raised to the power of the number of digits. For example, 371 is an Armstrong number since \(3^3+7^3+1^3 = 371\). The largest Armstrong number in decimal numbers has 39 digits. (115,132,219,018,763,992,565,095,597,973,522,401 is the largest) (Armstrong numbers are named for Michael F. Armstrong who named them for himself as part of an assignment to his class in Fortran Programming at the University of Rochester \)
I find it interesting that 39 = 3*13, and is the sum of all the primes from 3 to 13, 39=3+5+7+11+13, these are sometimes call ed straddled numbers.
39 is the smallest positive integer which cannot be formed from the first four primes (used once each), using only the simple operations +, -, *, / and ^. Prime Curios.
The number formed by concatenating the non-prime integers 1 through 39 is the smallest such prime: 1468910121415161820212224252627283032333435363839. Prime Curios.
\$ 3^{39} = 4052555153018976267 \$ is the smallest power of three which is pandigital, with all ten decimal digits. The number is 19 digits long. *@Fermat's Librarty
The 40th Day of the Year: in English forty is the only number whose letters are in alphabetical order.
There are 40 solutions on for the 7 queens problem. placing seven chess queens on a 7x7 chessboard so that no two queens threaten each other.
-40 is the temperature at which the Fahrenheit and Celsius scales correspond; that is, −40 °F = −40 °C.
Euler first noticed (in 1772) that the quadratic polynomial P(n) = n2 + n + 41 is prime for all non-negative numbers less than 40.
Paul Halcke noted in 1719 that the product of the aliquot parts of 40 is equal to 40 cubed. 1*2*4*5*8*10*20 = 64000 = 403. He found the same is true for 24.
And.... forty is the highest number ever counted to on Sesame Street.
40 = 2^3+5, the first three primes in order.
The 41st Day of the Year:
Euler (1772) observed that the polynomial f(x)= x2 + x + 41 will produce a prime for any integer value of x in the interval 0 to 39.
In 1778 Legendre realized that x2 - x + 41 will give the same primes for interval (1-40). n^2 + n + 41 is prime for n = 0 ... 39 and Is prime for nearly half the values of n up to 10,000,000. *John D. Cook
The smallest prime whose cube can be written as sum of three cubes in two ways (413 = 403 + 173 + 23 = 333 + 323 + 63). *Prime Curios
If you multiply 41 by any three digit number to produce a five digit number, every cyclic representation of that number formed by moving the last digit to the front is also divisible by 41. (for example 41*378 = 15,498. 41 will also divide 81,549; 98154; 49815; and 54,981 *The Moscow Puzzles
41 can be expressed as the sum of consecutive primes in two ways, (2 + 3 + 5 + 7 + 11 + 13), and the (11 + 13 + 17).
The sum of the digits of 41 (5) is the period length of its reciprocal, 1/41 =.0243902439,,, It is the smallest number with a period length of five.
41 is the largest known prime formed by the sum of the first Mersenne primes in logical order (3 + 7 + 31) *Prime Curios
Incredibly, if you take any two integers that sum to 41, a+b =41, then a^2 + b is a prime, for example, 20^2 + 21 = 421
Starting with 41, if you add 2, then 4, then 6, then 8, etc., you will have a string of 40 straight prime numbers. *Prime Curios
The 41st Mersenne to be found = 2^24036583-1. *Prime Curios
And even more from @Math Year-Round 41=1!+2!+3!+1¹+2²+3³
38 is also the magic constant in the only possible magic Yhexagon which utilizes all the natural integers up to and including 19. It was discovered independently by Ernst von Haselberg in 1887, W. Radcliffe in 1895, and several others. Eventually it was also discovered by Clifford W. Adams, who worked on the problem from 1910 to 1957. He worked on the problem throughout his career as a freight-handler and clerk for the Reading Rail Road by trial and error and after many years arrived at the solution which he transmitted to Martin Gardner in 1963. Gardner sent Adams' magic hexagon to Charles W. Trigg, who by mathematical analysis found that it was unique disregarding rotations and reflections.
 |
| *Wik |
The 39th Day of the Year, 39 is the smallest number with multiplicative persistence 3. [Multiplicative persistence is the number of times the digits must be multiplied until they produce a one digit number; 3(9)= 27; 2(7) = 14; 1(4)=4. Students might try to find the smallest number with multiplicative persistence of four, or prove that no number has multiplicative persistence greater than 11]
39 = 3¹ + 3² + 3³ *jim wilder @wilderlab An Armstrong (or Pluperfect digital invariant) number is a number that is the sum of its own digits each raised to the power of the number of digits. For example, 371 is an Armstrong number since \(3^3+7^3+1^3 = 371\). The largest Armstrong number in decimal numbers has 39 digits. (115,132,219,018,763,992,565,095,597,973,522,401 is the largest) (Armstrong numbers are named for Michael F. Armstrong who named them for himself as part of an assignment to his class in Fortran Programming at the University of Rochester \)
I find it interesting that 39 = 3*13, and is the sum of all the primes from 3 to 13, 39=3+5+7+11+13, these are sometimes call ed straddled numbers.
39 is the smallest positive integer which cannot be formed from the first four primes (used once each), using only the simple operations +, -, *, / and ^. Prime Curios.
The number formed by concatenating the non-prime integers 1 through 39 is the smallest such prime: 1468910121415161820212224252627283032333435363839. Prime Curios.
\$ 3^{39} = 4052555153018976267 \$ is the smallest power of three which is pandigital, with all ten decimal digits. The number is 19 digits long. *@Fermat's Librarty
The 40th Day of the Year: in English forty is the only number whose letters are in alphabetical order.
There are 40 solutions on for the 7 queens problem. placing seven chess queens on a 7x7 chessboard so that no two queens threaten each other.
-40 is the temperature at which the Fahrenheit and Celsius scales correspond; that is, −40 °F = −40 °C.
Euler first noticed (in 1772) that the quadratic polynomial P(n) = n2 + n + 41 is prime for all non-negative numbers less than 40.
Paul Halcke noted in 1719 that the product of the aliquot parts of 40 is equal to 40 cubed. 1*2*4*5*8*10*20 = 64000 = 403. He found the same is true for 24.
And.... forty is the highest number ever counted to on Sesame Street.
40 = 2^3+5, the first three primes in order.
The 41st Day of the Year:
Euler (1772) observed that the polynomial f(x)= x2 + x + 41 will produce a prime for any integer value of x in the interval 0 to 39.
In 1778 Legendre realized that x2 - x + 41 will give the same primes for interval (1-40). n^2 + n + 41 is prime for n = 0 ... 39 and Is prime for nearly half the values of n up to 10,000,000. *John D. Cook
The smallest prime whose cube can be written as sum of three cubes in two ways (413 = 403 + 173 + 23 = 333 + 323 + 63). *Prime Curios
If you multiply 41 by any three digit number to produce a five digit number, every cyclic representation of that number formed by moving the last digit to the front is also divisible by 41. (for example 41*378 = 15,498. 41 will also divide 81,549; 98154; 49815; and 54,981 *The Moscow Puzzles
41 can be expressed as the sum of consecutive primes in two ways, (2 + 3 + 5 + 7 + 11 + 13), and the (11 + 13 + 17).
The sum of the digits of 41 (5) is the period length of its reciprocal, 1/41 =.0243902439,,, It is the smallest number with a period length of five.
41 is the largest known prime formed by the sum of the first Mersenne primes in logical order (3 + 7 + 31) *Prime Curios
Incredibly, if you take any two integers that sum to 41, a+b =41, then a^2 + b is a prime, for example, 20^2 + 21 = 421
Starting with 41, if you add 2, then 4, then 6, then 8, etc., you will have a string of 40 straight prime numbers. *Prime Curios
The 41st Mersenne to be found = 2^24036583-1. *Prime Curios
Found this on Twitter (X) by Abakcus
The 42nd Day of the Year:
in The Hitchhiker's Guide to the Galaxy, the Answer to the Ultimate Question of Life, The Universe, and Everything is 42. The supercomputer, Deep Thought, specially built for this purpose takes 7½ million years to compute and check the answer. The Ultimate Question itself is unknown.
There is only one scalene triangle in simplest terms with integer sides and integer area of 42, it's perimeter is also 42. (There are only three integer (non-right) triangles possible with area and perimeter equal and all integer sides.)
42 is between a pair of twin primes (41,43) and its concatenation with either of them (4241, 4243) is also a prime, which means that 4242 is also between twin primes.
On September 6, 2019, Andrew Booker, University of Bristol, and Andrew Sutherland, Massachusetts Institute of Technology, found a sum of three cubes for \(42= (–80538738812075974)^3 + 80435758145817515^3 + 12602123297335631^3 \). This leaves 114 as the lowest unsolved case. At the beginning of 2019, 33 was the lowest unsolved case, but Booker solved that one earlier in 2019.
42 is the largest number n such that there exist positive integers p, q, r with 1 = 1 / n + 1 / p + 1 / q + 1 / r
In 1954, researchers at the University of Cambridge looked for solutions of the equation x^3 + y^3 + z^3 = k, with k being all the numbers from 1 to 100. As of late 2019, all numbers had been solved except 42, which proved to be especially challenging. That is until University of Bristol’s Professor Andrew Booker and MIT Professor Andrew Sutherland solved the equation with the help of @CharityEngine, a crowdsourcing platform that harnesses idle, unused computing power from more than 500,000 home PCs. *Mehmet Aslan
The 43rd Day of the Year.:
The McNuggets version of the coin problem was introduced by Henri Picciotto, who included it in his algebra textbook co-authored with Anita Wah.Picciotto thought of the application in the 1980s while dining with his son at McDonald’s, working the problem out on a napkin. A McNugget number is the total number of McDonald’s Chicken McNuggets in any number of boxes.The original boxes (prior to the introduction of the Happy Meal-sized nuggetboxes) were of 6, 9, and 20 nuggets.According to Schur’s theorem, since 6, 9, and 20 are relatively prime,any sufficiently large integer can be expressed as a linear combination of these three. Therefore, there exists a largest non-McNugget number, and all integers larger than it are McNugget numbers.That number is 43, so how many of each size box gives the McNugget number 44?
43 is the number of seven-ominoids. (shapes made with seven equilateral triangles sharing a common edge.)
In March of 1950, Claude Shannon calculated that there are appx \( \frac{64!}{32!} (8!)2(2!)6 \), or roughly 1043 possible positions in a chess match.
Planck time (~ 10-43 seconds) is the smallest measurement of time within the framework of classical mechanics. That means that if you could make one unique chess position in each Planck time, you could run through them all in one second.
What is the minimum number of guests that must be invited to a party so that there are either five mutual acquaintances, or five that are mutual strangers? (Sorry we still don't know :-{ But the smallest number must be 43 or larger). I think that means that for any number of points on a circle less than 43, if you colored every segment connecting two of them either red or black, there would be no complete graph of five vertices (K(5)) with all edges of the same color. [And there are 43 choose 5 or 962,598 possible choices of complete graphs to choose from.]
According to Benford's Law, the odds that a random prime begins with a prime digit is more than 43%
Every solvable configuration of the Fifteen puzzle can be solved in no more than 43 multi-tile moves (i.e. when moving two or three tiles at once is counted as one move)
43/100 or more exactly 3/7 shows up in a good approximation for the area of an equilateral triangle: "Gerbert of Aurillac (later Pope Sylvester II) referred to the equilateral triangle as “mother of all figures” and provided the formula A ≈ s^ 2 · 3/7 which estimates its area in terms of the length of its side to within about 1.003% ( N. M. Brown, The Abacus and the Cross, Basic, 2010, p. 109). 3/7 = .428571… sqrt(3)/4 = .433012
43 is the smallest (non-trivial) number that is equal to the consecutive powers of its digits, \(4^2 + 3^3 = 43\) . There are two more two digit numbers that fit this pattern. There are also two three digit year dates that fit if you restrict the powers to consecutive integers starting with 1.
And if 42 was the meaning of life, the universe, and everything, just imagine that 43 is MORE than that!
Jim Wilder shared \(43^7= 271818611107\) which has a digit sum of 43. Wonder how often you can find a multidigit number n so that n^k (for some k=2 through 9 will have a digit sum of n, or a digit sum which is m*n for some integer m? 27^3 = 19683 and 27^7 = 10460353203 came to mind. Rare, or not rare? When I checked 26^3, it also worked but not to seventh power. 53^7 =  also works, it seems
also works, it seems
The 44th Day of the Year:
there are 44 ways to reorder the numbers 1 through five so that none of the digits is in its natural place. This is called a derangement. The number of derangements of n items is an interesting study for students. Some historical notes from here. If you had five letters for five different people and five envelopes addressed to the five people, there are 44 ways to put every letter in the wrong envelope.
44 is the sum of the first emirp (prime which is prime with digits reversed) pair, 13 and 31.*Prime Curios
44 is the smallest number such that it and the next number are the product of a prime and another distinct prime squared (44 = 22*11 and 45 = 32*5).
All even perfect numbers greater than 6 end in 44 in base six, as do all powers of ten greater than 10. *Lord Karl Voldevive @Karl4MarioMugan (students should be encouraged to understand that the converse of these statements is not true by finding exceptions.)
44 and 45 form the first pair of consecutive numbers that are the product of a prime and the square of a prime. 44 = 2^2 * 11 and 45 = 3^2 * 5
44 is a palindrome in base ten, but not in any smaller base. Only three of the ninr two-digit palindromes in base ten are palindromes in any smaller base. Find them!
An Euler brick, named after Leonhard Euler, is a cuboid whose edges andface diagonals all have integer lengths. A primitive Euler brick is an Eulerbrick whose edge lengths are relatively prime.The smallest Euler brick, discovered by Paul Halcke in 1719, has edges( a,b,c ) = (44 , 117 , 240) and face diagonals 125, 244, and 267.
The 45th Day of the Year:
45 is the third Kaprekar number. (452 = 2025 and 20 + 25 = 45) The next two Kaprekar numbers both have two digits, can you find them? More unusual, it is also a Kaprekar number with third powers, 45^3 = 91125 and 9 + 11 + 25 = 45. But Wait! There's more. 45^4 = 4,100,625 and yes, 4 + 10 + 06 + 25 = 45. There is no other number known that is a Kaprekar number in all three powers.
45 is the 9th triangular number, the sum of the digits from 1 through 9.
45-2n for n=1 through 5 forms a prime
I found these on a post at the Futility Closet by Greg Ross: 452 = 2025 20 + 25 = 45 453 = 91125 9 + 11 + 25 = 45 454 = 4100625 4 + 10 + 06 + 25 = 45
45 is a palindrome in base 2 {101101} and base 8{55}
44 and 45 form the first pair of consecutive numbers that are the product of a prime and the square of a prime. 44 = 2^2 * 11 and 45 = 3^2 * 5
And a paradoxical anagram about 45; Over fifty = forty-five
The 45th row of Pascal's Arithmetic Triangle has 30 even numbers, the 60th row, has 45 even numbers. 45 is the smallest odd number n that has more divisors than n+1 and that has a larger sum of divisors than n+1
The 45th parallel, halfway between the North Pole and Equater, runs just outside my family home in Elk Rapids, Michigan.
The 46th Day of the Year:

46 is the largest even integer that cannot be expressed as a sum of two abundant numbers.
46 can be expressed as the sum of primes using the first four natural numbers once each, 46 = 41 + 3 + 241 + 23 = 64.
It can also be done to its reversal 41 + 23 = 64.
46 is the number of integer partitions of 18 into distinct parts.
46 is a palindrome in both base 4 and base 5
On Oct 29, 2008 the 46th discovered Mersenne Prime, then the world's largest prime was featured in Time magazine as one of the "great inventions" of the year. It was discovered by Smith, Woltman, Kurowski, et al. of the GIMPS (Great Internet Mersenne Prime Search) program.
Three more have been discovered since, one of which is smaller than this one, so while it was 46th discovered, it is 47th in rank. .
46^5 = 205962976, with a digit sum of 46. 46^8 = 20047612231936 also with a digit sum of 46. 46 is the second smallest number which has two expressions of n^k = digit sum of n.
The 47th Day of the Year:
47 is a Thabit number, named after the Iraqi mathematician Thâbit ibn Kurrah number, of the form 3 * 2n -1 (sometimes called 3-2-1 numbers). He studied their relationship to Amicable numbers. 47 is related to the amicable pair, (17296, 18416) All Thabit numbers expressed in binary end in 10 followed by n ones, 47 in binary is 101111. (The rule is that if p=3*2n-1 -1, q= 3*2n -1, and r = 9*2n-1 -1, are all prime, then 2npq and 2nr are amicable numbers.
3^3^3^3^3^3^3 has 47 distinct values depending on parentheses. *Math Year-Round @MathYearRound
666<sup>47</sup> has a sum of digits equal to the Beast Number, 666 *Prime Curios
479 can be written as the sum of distinct smaller 9th powers.*Prime Curios
"The 47 Society is an international interest-group that follows the occurrence and recurrence of the quintessential random number: 47. Many suspect that the coincidental nature of 47 carries some mystical, metaphysical and/or scientific significance." *http://www.47.net/47society/
47+4^4 +7^4=52^2
Mario Livio has pointed out that this date written month day as 216, 216=63 and also 216=33+43+53
The 47th day gives me a reason to include this brief story of Thomas Hobbes from Aubrey's "Brief Lives". The 47th proposition of Libre I of The Elements (The Pythagorean Theorem) seemed so obviously false to him that, in following the reasoning back, his life was changed:
He was (vide his life) 40 yeares old before he looked on geometry; which happened accidentally. Being in a gentleman’s library in . . . , Euclid’s Elements lay open, and ’twas the 47 El. libri I. He read the proposition. ‘By† G—,’ sayd he, ‘this is impossible!’So he reads the demonstration of it, which referred him back to such a propo- sition; which proposition he read. That referred him back to another, which he also read. Et sic deinceps,(and so back to the beginning) that at last he was demonstratively convinced of that trueth. This made him in love with geometry.
The 48th Day of the Year:
48 is the smallest number with exactly ten divisors. (This is an interesting sequence, and students might search for others. Finding the smallest number with twelve divisors will be easier than finding the one with eleven.)
48 is also the smallest even number that can be expressed as a sum of two primes in 5 different ways: If n is greater than or equal to 48, then there exists a prime between n and 9n/8 This is an improvement on a conjecture known as Bertrand's Postulate. In spite of the name, many students remember it by the little rhyme, "Chebyshev said it, but I'll say it again; There's always a prime between n and 2n ." Mathematicians have lowered the 2n down to something like n+n.6 for sufficiently large numbers.
48 is the smallest betrothed (quasi-amicable) number. 48 and 75 are a betrothed pair since the sum of the proper divisors of 48 is 75+1 = 76 and the sum of the proper divisors of 75 is 48+1=49. (There is only a single other pair of betrothed numbers that can be a year day)
And 48 x 48 = 2304 but 48 x 84 = 4032. (Others like this???)
If you picked four prime numbers so that any collection of three of them had a prime sum, then the smallest sum you could get adding all four primes, is 48. (5, 7, 17, 19). Can you find the next smallest?(suitable for middle school students to explore as there are many with modest size numbers)
In 1719 Paul Halcke observed that the product of the aliquot divisors of 48 is equal to the fourth power of 48. 1*2*3*4*6*8*12*16*24= 5,308,416= 484. 48 and 80 are the only two year dates for which this is true.
48 is a Harshad Number from the Sanskrit for "joy-giver", since it is divisible by the sum of its digits. It is also one of the numbers cubed in the 11th Taxicab number 110656 = 40 ^3 + 36 ^3 = 48 ^3 + 4 ^3.
48 x 159 = 5346 And uses all nine digits
The 49th Day of the Year:
lots of numbers are squareful (divisible by a square number) but 49 is the smallest number so that it, and both its neighbors are squareful. (Many interesting questions arise for students.. what's next, can there be four in a row?, etc)
And Prof. William D Banks of the University of Missouri has recently proved that every integer in base ten is the sum of 49 or less palindromes. (August 2015) (Building on Prof. Banks groundbreaking work, by February 22, 2016 JAVIER CILLERUELO AND FLORIAN LUCA had proved that for any base > 4 EVERY POSITIVE INTEGER IS A SUM OF THREE PALINDROMES )
The 49th Mersenne prime is discovered. On Jan 19th, 2016 The GIMPS program announced a new "largest known" prime, 274,207,281 -1. called M74,207,281 for short, the number has 22,338,618 digits.
49 is the smallest square which is the sum of three consecutive primes.49= 17 + 19 + 23
49 is the first square where the digits are squares, What's next?
1, 25, 49 is the smallest arithmetic progression of three squares that I have ever found. 4, 100, and 196 come next . Is there one starting with nine? It is proven that an arithmetic progression of four squares in not possible.
If you square 49, and take the sum of the digits of that square, you have 7, the square root of 49. How common is this?
If you square 49, and take the sum of the digits of that square, you have 7, the square root of 49. How common is this?
Student's are reminded that 8 x 6 + 1 is 49, an example of a beautiful mathematical truth that 8 x T + 1 is a square for any triangular number.
1 / 49 = 0.0204081632 6530612244 8979591836 7346938775 51 and then repeats the same 42 digits. It's better than it looks. Write down all the powers of two, and then index them two to the right and add.
1, 25, 49 is the smallest arithmetic progression of three squares that I have ever found. 4, 100, and 196 come next . Is there one starting with nine? It is proven that an arithmetic progression of four squares in not possible.
1 / 49 = 0.0204081632 6530612244 8979591836 7346938775 51 and then repeats the same 42 digits. It's better than it looks. Write down all the powers of two, and then index them two to the right and add.
 |
| *Wik |
1, 25, 49 is the smallest arithmetic progression of three squares that I have ever found. 4, 100, and 196 come next . Is there one starting with nine? It is proven that an arithmetic progression of four squares in not possible.
Everyone knows 25 is the hypotenuse of a Pythagorean right triangle with legs of 7 and 24. A Pythagorean triangle can never have two sides that are squares. When a square occurs as the shorter leg, and interesting pattern occurs:
leg leg hypotenuse
9 40 41
25 312 313
49 1200 1201
81 3280 3281
good geometry students may already know that any (including all the squares above) odd number n larger than one, is the short leg of a right triangle with a difference of one between the other leg and the hypotenuse. The square of the odd leg is the sum of the other leg and hypotenuse
ODD Leg Even Leg Hypotenuse
3 4 5 4 + 5 = 3^2
5 12 13 12 + 13 = 5^2
7 24 25 24 + 25 = 7^2
The 50th Day of the Year:
50 is the smallest number that can be written as the sum of two squares in two distinct ways 50 = 49 + 1 = 25 + 25. *Tanya Khovanova, Number Gossip (What is the next, or what is the smallest number that can be written as the sum of two squares in three distinct ways?
It is also the sum of three squares, 3^2 + 4^2 + 5^2 = 50 and of four squares, 1^2 + 2^2 + 3^2 + 6^2 = 50
You can use the first nine consecutive primes to express 50 as the sum of primes in two different ways, :50 = 2 + 5 + 7 + 17 + 19 = 3 + 11 + 13 + 23.
The number 50 is somewhat responsible for the area of number theory about partitions. In 1740 Philip Naudé the younger (1684-1747) wrote Euler from Berlin to ask “how many ways can the number 50 be written as a sum of seven different positive integers?” Euler would give the answer, 522, within a few days but would return to the problem of various types of partitions throughout the rest of his life.
There is no solution to the equation φ(x) = 50, making 50 a nontotient (there is no integer, k, that has exactly 50 numbers below it that do not share a divisor with k, other than 1).
The 51st Day of the Year:
51 is the number of different paths from (0,0) to (6,0) made up of segments connecting lattice points that can only have slopes of 1, 0, or -1 but so that they never go below the x-axis. These are called Motzkin Numbers.
\(\pi(51) = 15\), the number of primes less than 51 is given by it's reversal, 15, and both numbers are products of Fermat Primes.
Jim Wilder pointed out that 51 is the smallest number that can be written as a sum of primes with the digits 1 to 5 each used once 2 + 3 + 5 + 41 = 51 (Students might explore similar problems using first n digits 2-9)
51 can be expressed as the sum of four primes using only the digits from 1-5, 51 = 2 + 3 + 5 + 41.
A triangle with sides 51, 52 and 53 has an integer area 1170 units2. These are called Heronian Triangles, or sometimes Super Heronian Triangles but I prefer to call them after the earliest study of them I have found, and will refer to them as Fleenor-Heronian triangles . (Guess I shouldn't be, but surprised how all of the triangles I could find with consecutive integer sides and integer area have final digits of 1,2,3 or 3,4,5) There are an infinite number of these with consecutive integers for sides. To find the even side, just take the expansion of \( (2 + \sqrt{3})^n \),and sum the rational terms, then double it to get the even side. The first three are 2, 7, giving us the even side of a 3,4,5 triangle and the 13, 14, 15 triangle. And if you expand \( (2 + \sqrt{3})^4 \) you get \( 8 + 12 \sqrt{3} + 3(2)3 + \sqrt{3^3} =26\) and we get the center side of the triangle above. (My thanks to @expert_says on twitter who sent me a link to two nice papers on this) (more notes about this in Day 52)
And like any odd number, it is the sum of two consecutive numbers, 25+26 , and the difference of their squares \(26^2 - 25^2\)
And I just found this unusual reference, "Don’t be baffled if you see the number 51 cropping up in Chinese website names, since 51 sounds like 'without trouble' or 'carefree' in Chinese." at the Archimedes Lab
Since 51 is the product of the distinct Fermat primes 3 and 17, a regular polygon with 51 sides is constructible with compass and straightedge, the angle π / 51 is constructible, and the number cos π / 51 is expressible in terms of square roots.
The 52nd Day of the Year,
The month and day are simultaneously prime a total of 52 times in a non-leap year. *Tanya Khovanova, Number Gossip How many times in a leap year ?
52 is also the maximum number of moves needed to solve the 15 puzzle from the worst possible start. *Mario Livio
52 is the number of 8-digit primes (on a calculator) that remain prime if viewed upside down, in a mirror, or upside down in a mirror. *Prime Curios
There are 52 letters in the names of the cards in a standard deck: ACE KING QUEEN JACK TEN (This also works in Spanish. any other languages for which this is true?) *Futility Closet
52 is called an "untouchable" number, since there is no integer for which the sum of its proper divisors sum to 52. Can you find another? Euler said they were infinite.
A triangle with sides 51, 52 and 53 has an integer area 1170 units2. These are called Heronian Triangles, or sometimes I call them Sang-Heronian triangles after the earliest study I know about them by Edward Sang of Edinburgh, Scotland in 1864. They have consecutive integer sides Each of these triangles can be partitioned into two Heronian right triangles by the altitude to the even side. It seems that in all such triangles, the altitude will divide the even base into two sides whose lengths differ by 4. For this one, the two right triangle bases will be 26-2 and 26+2. To find the height of the triangle, we use the simple A=1/2 b*h , so 1170 = 26*h, and we get h = 45. So the two right triangles have sides of 24, 45, 51 with area of 540 sq units; and 28, 45, 53 with area of 630 sq units. In every pair of right triangles formed by the altitude, one of them is a Primitive Pythagorean Triangle. In this one the PPT is 28, 45, 53.
The 53rd Day of the Year:
The 53rd day of the year; the month and day are both prime a total of 53 times in every leap year, but not today.
If you reverse the digits of 53 you get its hexadecimal representation; no other two digit number has this quality. You also get the sum of the divisors of 53^3.
The sum of the first 53 primes is 5830, which is divisible by 53. It is the last year day for which n divides the sum of the first n primes. (what were the others?)
53 is the sum of 5 consecutive numbers, with an average interval of 3
If you raise 2^n starting at one, and searching for a number with two adjacent zeros, you want find one until n = 53.
53 is the smallest prime p such that 1p1 (ie, 1531) , 3p3, 7p7 and 9p9 are all prime.(Can you find the 2nd smallest?) Raj Madhuram suggested 2477 is the second smallest of these, and offered the wonderful term, "Sandwich Primes." (Raj actually found five more four digit primes that are "sandwich-able". We leave them as a challenge for the reader. )
53 is the smallest prime number that does not divide the order of any sporadic group *Wik
A triangle with sides 51, 52 and 53 has an integer area 1170 units2. These are called Heronian Triangles, or sometimes Fleenor-Heronian Triangles, because they have sides of consecutive integers. The even side of these triangles is related to a classic equation from Diophantus' Arithmetic (AD 200's). This one is now known as a type of Pell Equation \( x^2 - 3y^2 = 1\). For example it is easy to see that x=2, y=1 is a solution, and the x=2, doubled becomes the even side in the 3,4,5 Triangle. The triangle with even side of 52, is from the solutions x=26, y=15. If you explore the successive rational convergents to the \(\sqrt{3}\), these occur as every other term in that series. \( \frac{2}{1} , \frac{5}{3}, \frac{7}{4}, \frac{19}{11}, \frac{26}{15}...\).
Computer Geeks (the capital shows respect) may know that 53 has a prime ASCII code, 3533. It is the smallest prime for which that is true.
The floor function of \(e ^\phi \) is 53.
You may know that with the traditional Birthday Problem, 23 people reduces the chance of not finding a match to about 1/2. Increase that number to 53, and the probability of no match is about 1/53.
53 is a self number, since it cannot be formed as the sum of any integer and its digits.
another from Jim Wilder, the sum of the digits of \( 53^7 = 1174711139837\) is 53.
53 appears twice in one of the most incredible factorizations I've ever known. The number 13532385396179 has prime factors of 13, 53^2, 3853, and 96179, using exactly the same digits in order when you include the square. *Alon Amit
The 54th Day of the Year:
54 is the smallest number that can be written as the sum of 3 squares in 3 ways.(Well, go on, find all three ways!)
And the 54th Prime Number, is the smallest number expressible as the sum of 3 cubes in 3 ways. *Prime Curios
There are 54 ways to draw six circles through all the points on a 6x6 lattice. *gotmath.com
54 is the fourth Leyland number, after mathematician Paul Leyland. Leyland numbers are numbers of the form \(x^y + y^x \) where x,y are both integers greater than 1.
And the Sin(54o) is one-half the golden ratio.
Of course, we should add that the Rubiks Cube has 54 squares.
Not sure how he finds these, but Jim Wilder just keeps coming up with them; \(54^6\) = 24794911296, and the sum of those digits is 54. (also see day 53)
The 55th Day of the Year:
55 is the largest triangular number that appears in the Fibonacci Sequence. (Is there a largest square number?)
55 is also a Kaprekar Number: 55² = 3025 and 30 + 25 = 55 (Thanks to Jim Wilder)
And speaking of 52, Everyone knows that 32 + 42 = 52, but did you know that 332 + 442 = 552 But after that, there could be no more.... right? I mean, that's just too improbable, so why is he still going on like this? You don't think......Nah.
55 is the only year day that is both a non-trivial base ten palindrome and also a palindrome in base four.
Every number greater than 55 is the sum of distinct primes of the form 4n + 3. *Prime Curios Someone help me out here. If this is true, then since 55=37 + 13 + 5 , should this say greater than or equal to 55?
55 is a square pyramidal number, the sum of the squares of the first 5 positive integers.
The first squared square was published in 1938 by Roland Sprague who found a solution using several copies of various squared rectangles and produced a squared square with 55 squares, and side lengths of 4205
No squared square can be made with less than 21 squares *Wik
The 56th Day of the Year:
There are 56 normalized 5x5 Latin Squares (First row and column have 1,2,3,4,5; and no number appears twice in a row or column. There are a much smaller number of 4x4 squares, try them first)
56 is the sum of the first six triangular numbers (56= 1 + 3 + 6 + 10 + 15 + 21) and thus the sixth tetrahedral number.
56 is also the sum of six consecutive primes. 3 + 5 + 7 + 11 + 13 + 17
56 is the maximum determinant in an 8 by 8 matrix of zeroes and ones.
If you multiply all the composite numbers up to and including 56, and add one, you get a prime number...... with 56 digits.*Prime Curios
56 can be expressed as the sum of two primes in two different ways using only numbers that end in 3.
|$ 56^7 = 1727094849536 \$ is the smallest seventh power that will produce a pandigital (all digits 0-9 in decimals) number. It has 13 digits. *@Fermat's Library (It is actually possible to get all ten digits in a ten digit number that is the square of a five digit number, 32043^2= 1026753849
There are 56 ways to express 11 as the sum of positive integers
Fifty-Six, Arkansas is a city in Stone County in North Central Arkansas. When founding the community in 1918, locals submitted the name "Newcomb" for the settlement. This request was rejected, and the federal government internally named the community for its school district number (56).*Wik.
The 57th Day of the Year:
57(base ten) is written with all ones in base seven. It is the last day this year that can be written in base seven with all ones.(What is the last day of the year that can be written with all ones in base two,... base three?)
57 is the maximum number of regions inside a circle formed by chords connecting 7 points on the circle. Students might ask themselves why this is the same as the first five numbers in the sixth row of Pascal's triangle.
57 is the number of permutations of the numbers 1 to 6 in which exactly 1 element is greater than the previous element (called a permutations with 1 "ascents").
57 letters and spaces are required to write the famous prime number 6700417 in English. The number was one of the factors of \(F(5)=2^{2^5}+1 \) Fermat had conjectured that all such "Fermat Numbers" were prime. In 1732, Euler showed that F(5) was the product or 641 times 6700417. Euler never stated that both numbers were prime, and historians still disagree about whether he knew, or even suspected, that it was.
57 is the maximum number of possible interior regions formed by 8 intersecting circles.
The number of ways of coloring the faces of a cube with 3 different colors is 57. For coloring a cube with n colors, the number of possible colorings is given by
57, is sometimes known as Grothendieck's prime. The explanation is given in Amir D. Aczel's last book, Finding Zero. Grothendieck had used primes as a framework on which to build some more general result when:
Among the first 1000 primes, more numbers end in 57 than any other two digit ending.
57 is the third year day which remains prime if a 5 is inserted anywhere in its digits except at the end. Can you find the smaller pair? And it's the sixth year day which can have a 7 inserted anywhere, including at the end, so 757, 577 are both prime.
57 is a repdigit in base 7, \( 57_{10}= 111_7 \)
Among the first 1000 primes, more numbers end in 57 than any other two digit ending.
57 is the third year day which remains prime if a 5 is inserted anywhere in its digits except at the end. Can you find the smaller pair? And it's the sixth year day which can have a 7 inserted anywhere, including at the end, so 757, 577 are both prime.
57 is a repdigit in base 7, \( 57_{10}= 111_7 \)
The famous Heinz 57 name was created by the owner, Henry Heinz, in 1896. At the time he says he chose 57 because he thought 5 was lucky, and his wife's favorite lucky number was 7. (He had also told other reasons for the name.)
The 58th Day of the Year:
58 is the sum of the first seven prime numbers.
It is the fourth smallest Smith Number. (Find the first three. A Smith number is a composite number for which the sum of its digits equals the sum of the digits in its prime factorization, including repetition. 58 = 2*29, and 5+8= 2+2+9.) Smith numbers were named by Albert Wilansky of Lehigh University. He noticed the property in the phone number (493-7775) of his brother-in-law Harold Smith. 58 is also the smallest Smith Numer with the sum of it's digits prime. And the two digits and their sum form consecutive Fibonacci numbers.
If you take the number 2, square it, and continue to take the sum of the squares of the digits of the previous answer, you get the sequence 2, 4, 16, 37, 58, 89, 145, 42, 20, 4, and then it repeats. See what happens if you start with other values than 2, and see if you can find one that doesn't produce 58.
The Greeks knew 220 and 284 were Amicable in 300 BCE. By 1638 two more pairs had been added. Then, in 1750 in a single paper, Euler added 58 more.
The 59th Day of the Year:
59 is the center prime number in a 3x3 prime magic square that has the smallest possible total for each row, column and diagonal, 177. It was reportedly found by Rudolf Ondrejka. In 1913, English puzzle writer Henry Dudeney gave an order 3 prime magic square that used the number 1. Although is was commonly included as a prime then, present day convention no longer considers it a prime.
The letters I, L, and X in Roman numerals can only be used three different ways, all three are prime numbers. LIX evaluates to be 59.
59 is the sum of three consecutive primes, 17 + 19 + 23 = 59
 59 divides the smallest composite Euclid number 13# + 1= 13*11*7*5*2 + 1 = 59*509 (the symbol for a primorial, n#, means the product of all primes from n down to 2)Euclid used numbers of the form n#+1 in his proof that there are an infinite number of primes.
59 divides the smallest composite Euclid number 13# + 1= 13*11*7*5*2 + 1 = 59*509 (the symbol for a primorial, n#, means the product of all primes from n down to 2)Euclid used numbers of the form n#+1 in his proof that there are an infinite number of primes.And at the right is one of the 59 stellations of the icosahedron.
Now for some nice observations from Derek Orr@MathYearRound: 5^59 - 4^59 is prime.
4^59 - 3^59 is prime.
3^59 - 2^59 is prime.
Four Amicable Number pairs were known before Euler, He found 59 pairs. *Prime Curios (OK, a page at Princeton by William Dunham says he found 58, and Wolfram Alpha says he found 60. Pick your favorite.)
Fun Time! If you use the digits 1,2,3,4,5,6,7,8,9 in order and separate digits by * or +, the smallest prime you can get is 59. What other primes can you produce?
The first 59 digits of 58^57 form a prime.
An article in Quanta Magazine said that all the tetrahedra with rational dihedral angles are found, and there are 59 distinct tetrahedra, plus two infinite groups. A graph of all of them distinct ones is at the start of their link here.
The 60th Day of the Year:
60 is the smallest composite number which is the order of a simple group.
60 is the smallest number that is the sum of two odd primes in 6 ways.(Collect the whole set)
The final digits of the Fibonacci sequence have period 60. F(n) and F(n+60) both end in the same digit.
7! is the smallest # with 60 divisors.
If you list all the divisors of numbers less than, and relatively prime to 60, they are either prime, a power of a prime, or 1. 60 is the largest number for which this is true. *Prime Curios
60 is the largest known integer for which which can not be expressed by three distinct primes in the form p*q+r
There are four Archimedean solids with 60 vertices , : the truncated icosahedron, the rhombicosidodecahedron, the snub dodecahedron, and the truncated dodecahedron.
Oh, and Pi day is coming up in a couple of weeks, so ... suppose you were scrolling through the digits of pi and wondered how long it would take until you found a string of ten digits that had all ten of 0 through nine in it... Benjamin Vitale @BenVitale thought to find out and :
You can arrange the whole numbers from 1 to 60 into pairs so that the sum of the numbers in each pair is a perfect square; in fact, you can do it in 4,366,714 ways. Here is one of those presented in a pretty fashion using only five squares for the sums. *Gordon Hamilton, Kiran S. Kedlaya, and Henri Picciotto; Square–Sum Pair Partitions(Won the George Polya Prize from MAA for 2016)
The 60th Day of the Year:
60 is the smallest composite number which is the order of a simple group.
60 is the smallest number that is the sum of two odd primes in 6 ways.(Collect the whole set)
The final digits of the Fibonacci sequence have period 60. F(n) and F(n+60) both end in the same digit.
7! is the smallest # with 60 divisors.
If you list all the divisors of numbers less than, and relatively prime to 60, they are either prime, a power of a prime, or 1. 60 is the largest number for which this is true. *Prime Curios
60 is the largest known integer for which which can not be expressed by three distinct primes in the form p*q+r
There are four Archimedean solids with 60 vertices , : the truncated icosahedron, the rhombicosidodecahedron, the snub dodecahedron, and the truncated dodecahedron.
Oh, and Pi day is coming up in a couple of weeks, so ... suppose you were scrolling through the digits of pi and wondered how long it would take until you found a string of ten digits that had all ten of 0 through nine in it... Benjamin Vitale @BenVitale thought to find out and :
You can arrange the whole numbers from 1 to 60 into pairs so that the sum of the numbers in each pair is a perfect square; in fact, you can do it in 4,366,714 ways. Here is one of those presented in a pretty fashion using only five squares for the sums. *Gordon Hamilton, Kiran S. Kedlaya, and Henri Picciotto; Square–Sum Pair Partitions(Won the George Polya Prize from MAA for 2016)


















No comments:
Post a Comment