The 241st day of the year; 241 is the larger of a pair of twin primes. The larger of a pair of twin primes is always one more than a multiple of six; the smaller is always one less than a multiple of six.
2+4+1 is prime. 241 is the 53rd prime. (53 is also prime) *Derek Orr
241 is also The smallest prime p such that p plus the reversal of p equals a palindromic prime. 241 + 142 = 383; which is a prime palindrome.
And it is the largest known prime p such that the reversal of (p! + p) is prime. (241! + 241 ends with a string of fifty-five zeros, and then 241 : 980360372638941007038951797078339359751464353463061342202811 188548638347461066010066193275864531994024640834549254693776 854464608509281547718518965382728677985343589672835884994580 815417004715718468026937051493675623385569404900262441027874 255428340399091926993707625233667755768320823071062785275404 107485450075779940944580451919726756974354635829128751944137 27644867102380111026020691554782580923999494640500736 0000000000000000000000000000000000000000000000000000000241 and if you write the reversal of that, it's prime.
241 is the smallest non-palindromic prime which can be expressed as sum of a number and its reverse, i.e., 241 = 170 + 071. *Prime Curios.
241 is the smallest prime p such that p^7 can be written as the sum of seven consecutive primes. *Prime Curios
241 can be written as the sum of three double digit emirps, 71 + 73 + 97. There is no larger number for which this is true. *Prime Curios
241 = 121^2 - 120^2.
241 = 15^2 + 4^2 which means 241 is a Pythagorean Prime.
241 is a palindrome in duodecimal, base 12 (181) and a repdigit in base 15(111)
P. Honaker at Prime Curios points out that the sequence of primes formed by n!+239 begins, 241, 263, 359... Maybe I mis-searched but I did not find this sequence in OEIS. Seems like a good computer programming project for students, pick a prime and find primes of the form n! + p
John Cook posted that "if k is relatively prime to b, there is a multiple of k whose base b representation contains all ones. If I understand that then since 241 is prime, it is relatively prime to ten. Can you find the base ten multiple of k that has all ones for its digits? Be the first to share the answer with me and get imortality by being listed here. I think it must be a very large multiple of 241.
, The 242nd Day of the Year
242 has six divisors...but 243, 244, and 245 also each has six divisors. 242 is the smallest integer to begin a run of four consecutive integers all of which have the same number of divisors. (What is the smallest integer that begins a run of three consecutive integers with an equal number of divisors?)
242 is not only a palindrome in base ten, it is also a palindrome (and repdigit) in base 3, \( 22222_3\) and base 7, \( 464_7 \). (What palindrome in base ten is also a palindrome in the most other bases 2-9?)
242 = 2 x 11^2, it is divisible by 2, 11, 22, 121 all of which are also palindromes.
242 is the smallest number that is between a prime and a fifth power of a prime.*Prime Curios
242 is one more than the larger of a twin prime pair, and 6 x 242 is between a prime pair.
242 is a multiple of 11, and if you sum the digits in base 100 (ie, 2 + 42) it is also divisible by 11.
242 is the nth prime, + n for n = 45.
The 243rd Day of the Year
243 is the largest three digit number that can be expressed as a fifth power (35). It is the smallest p^q where p and q are twin primes.
243 is also the sum of five consecutive prime numbers (41 + 43 + 47 + 53 + 59).
243 is the sum of palindrome primes, 11+101+131 *Prime Curios
243 is the sum of 4# + 3# + 1# + 0#, where n# is the product of the first n primes and 0#=1, 243 = 210 + 30 + 2 + 1 *Prime Curios
Venus' day is 243 Earth days. *Derek Orr
243 is a Harshad number, divisible by the sum of it's digits, and every permutation of its digits is also.
243, like all odd numbers, is the difference in consecutive squares, 122^2-121^2 = 243, because it is 3 mod6 it is also the difference of two squares of integers that differ by 3, 42^2 - 39^2. And with multiple 3's you get more differences, 18^2 - 9^2
243 is a palindrome in base 8 (363)
3^3 + 6^3 = 243
On April 14, 2014, Almost exactly a year after Yitang Zhang announced a proof (see April 17) that there are infinitely many pairs of prime numbers which differ by 70 million or less Terrance Tao's online group attack on the problem reduced the number to 243. Zhang's proof is the first to establish the existence of a finite bound for prime gaps, resolving a weak form of the twin prime conjecture.
The 244th Day of the Year
244 is the smallest number (besides 2) that can be written as the sum of 2 squares (10^2 + 12^2) or the sum of two 5th powers(5^3 + 1^3) *What's Special about this number It is the second smallest number where both squares are squares of numbers with more than one prime factor.
244 is (the second) anti-perfect. The proper divisors are 1, 2, 4, 61, and 122, & adding their reversal is 1 + 2 + 4 + 16 + 221 = 244. *Jim Wilder @wilderlab (244 is the smallest multi-digit anti-perfect number; There is one more year day which is anti-perfect.... don't just sit there, go find it!)
244 is also the sum of three cubes, \( 244 = 1^3 + 3^3 + 6^3 \)
244 is "power friendly" with 136. \(244 =1 ^3 + 3^3 + 6^3\) and \(136 = 2^3 + 4^3 + 4^3\)
244 = 2^2 x 61, and because it is divisible by four, it is the difference of two squares, 62^2 - 60^2.
244 is a palindreome in base 3 (100001) and base 11 (202)
244 is the 7th number in the "double and reverse" sequence, 1, 2, 4, 8, 61, 221, 244, ... *Wikipedia
244 is the sum of four consecutive triangular numbers, (45 + 55) + (66 + 78) = 10^2 + 12^2
The 245th Day of the Year
245 is the fifth StellaOctangula number. The sum of the 5th octahedral number (85) and eight of the fourth tetrahedral numbers (20). 245 =85 + 8 (20)
245 is also the sum of three consecutive squares, \(245 = 8^2 + 9^2 + 10^2 \)
There are 245 odd entries in the first 33 rows of the Arithmetic Triangle.
245 is also the 46th prime plus 46, 199+46=245 (is there a mathematical significance for these numbers, or just a nice curiosity? Serious question.)
The third largest known pair of "cousin primes, p and p+4) is given by the product of all odd numbers up to 245 +/- 2, they each have 241 digits
245 is the aliquot sum (sum of the divisors less than n) of any of these numbers: 723, 1195, 2563, 3859, 9259, 10123, 12283, 14659 and 14803.
The smallewst base that makes 245 base b a palindrome is base 34, where it is the repdigit 77. After base 36= 26 + 9 there are no letters left, how do thewy indicate a number in bases greater than 37 that is 37, 38, etc.
245, since it ends in 5 and is bigger than 25, is the difference of two squares of integers that differ by 5.. 245 = 27^2 - 22^2. Like all odd numbers, it is the difference of consecutive squres, 123^2 - 122^2.
The 246th Day of the Year
246 is a sphenic (wedge) composite since it is the product of three distinct prime factors, 246 = 2x3x41. (what would be the next sphenic number?)
246 is also equal to the sum 9C2 + 9C4 + 9C6 (9 choose 2,4,6)
246 = 233 + 13 (13th Fibonacci number plus 13) *Derek Orr@Derektionary
246 is the smallest number whose complete factorization contains the first four digits (and no others) 246 = 2*3*41
Algebra Fact @AlgebraFact points out that: "Tao, et all, have proved that there are infinitely many primes 246 apart." On the way to proving, hopefully, that there are an infinity of twin primes.
246 is an untouchable number, a number that can not be formed from the proper divisors of any number. Paul Erdos proved there are an infinite number of them. The early ones are 2, 5, 62, 88, 96... There are only 29 untouchable year dates, but very unevenly divided by the century groups. 5 below 100, 5 more before 200, then 12 between 200 and 300, and 8 between 300 and 400.
246 is a palindrome in base 5(1441) and base 9(303)
246 can be expressed as the sum of three (not distinct) squares. 14^2 + 5^2 + 5*2
The "aliquot sequence) of a number is the chain of results following from iterating the sum of the aliquot factros. The Chain for 246 is 258, 270, 450, 759, 393, 135, 105, 87, 33, 15, 9, 4, 3, 1, 0. *Wikipedia
246 is the average of two primes br />
The 247th Day of the Year
247 is the smallest number which can be expressed as the difference between two integers such that together, they contain all digits 0-9. (50123 - 49876)
The digits of 247 sum to its smallest prime factor (247 = 13 x 19 and 2 + 4 + 7 = 13) *Prime Curios 247 = 13 x 19. The two factors are prime when concatenated in either order.(How many of the composite days of the year sum to one of their prime factors?)
The digits of 247 add up to 13, which divides 247 making it a Harshad (Joy-giver) number. It is the smallest Hareshad Nummber with a digit sum of 13.
The mathematician and philosopher Alex Bellos suggested in 2014 that a candidate for the lowest uninteresting number would be 247 because it was, at the time, "the lowest number not to have its own page on English Wikipedia". *Wikipedia (OF course that fact makes it interesting, proving that there are no uninteresting numbers.
247 is the difference of consecutive squares, 144^2 - 143^2 , and 16^2 - 3^2 also.
247 can be written in three different ways as the sum of consecutive natural numbers, 4 + ... + 22 is one.
247 is the 13th Pentagonal number ( n x (3n-1)/2) . The average of the first n pentagonal numbers, is the nth Triangular number. Like all pentagonal numbers, it is the sum of the n consecutive numbers starting with n. so the 13th pentagonal number is 13 + 14 + 15 + ... 25 = 247
247 + the product of its digits, 56, is 303, a palindrome.
The 245th Day of the Year
245 is the fifth StellaOctangula number. The sum of the 5th octahedral number (85) and eight of the fourth tetrahedral numbers (20). 245 =85 + 8 (20)
245 is also the sum of three consecutive squares, \(245 = 8^2 + 9^2 + 10^2 \)
There are 245 odd entries in the first 33 rows of the Arithmetic Triangle.
245 is also the 46th prime plus 46, 199+46=245 (is there a mathematical significance for these numbers, or just a nice curiosity? Serious question.)
The third largest known pair of "cousin primes, p and p+4) is given by the product of all odd numbers up to 245 +/- 2, they each have 241 digits
245 is the aliquot sum (sum of the divisors less than n) of any of these numbers: 723, 1195, 2563, 3859, 9259, 10123, 12283, 14659 and 14803.
The smallewst base that makes 245 base b a palindrome is base 34, where it is the repdigit 77. After base 36= 26 + 9 there are no letters left, how do thewy indicate a number in bases greater than 37 that is 37, 38, etc.
245, since it ends in 5 and is bigger than 25, is the difference of two squares of integers that differ by 5.. 245 = 27^2 - 22^2. Like all odd numbers, it is the difference of consecutive squres, 123^2 - 122^2.
The 246th Day of the Year
246 is a sphenic (wedge) composite since it is the product of three distinct prime factors, 246 = 2x3x41. (what would be the next sphenic number?)
246 is also equal to the sum 9C2 + 9C4 + 9C6 (9 choose 2,4,6)
246 = 233 + 13 (13th Fibonacci number plus 13) *Derek Orr@Derektionary
246 is the smallest number whose complete factorization contains the first four digits (and no others) 246 = 2*3*41
Algebra Fact @AlgebraFact points out that: "Tao, et all, have proved that there are infinitely many primes 246 apart." On the way to proving, hopefully, that there are an infinity of twin primes.
246 is an untouchable number, a number that can not be formed from the proper divisors of any number. Paul Erdos proved there are an infinite number of them. The early ones are 2, 5, 62, 88, 96... There are only 29 untouchable year dates, but very unevenly divided by the century groups. 5 below 100, 5 more before 200, then 12 between 200 and 300, and 8 between 300 and 400.
246 is a palindrome in base 5(1441) and base 9(303)
246 can be expressed as the sum of three (not distinct) squares. 14^2 + 5^2 + 5*2
The "aliquot sequence) of a number is the chain of results following from iterating the sum of the aliquot factros. The Chain for 246 is 258, 270, 450, 759, 393, 135, 105, 87, 33, 15, 9, 4, 3, 1, 0. *Wikipedia
246 is the average of two primes br />
The 247th Day of the Year
247 is the smallest number which can be expressed as the difference between two integers such that together, they contain all digits 0-9. (50123 - 49876)
The digits of 247 sum to its smallest prime factor (247 = 13 x 19 and 2 + 4 + 7 = 13) *Prime Curios 247 = 13 x 19. The two factors are prime when concatenated in either order.(How many of the composite days of the year sum to one of their prime factors?)
The digits of 247 add up to 13, which divides 247 making it a Harshad (Joy-giver) number. It is the smallest Hareshad Nummber with a digit sum of 13.
The mathematician and philosopher Alex Bellos suggested in 2014 that a candidate for the lowest uninteresting number would be 247 because it was, at the time, "the lowest number not to have its own page on English Wikipedia". *Wikipedia (OF course that fact makes it interesting, proving that there are no uninteresting numbers.
247 is the difference of consecutive squares, 144^2 - 143^2 , and 16^2 - 3^2 also.
247 can be written in three different ways as the sum of consecutive natural numbers, 4 + ... + 22 is one.
247 is the 13th Pentagonal number ( n x (3n-1)/2) . The average of the first n pentagonal numbers, is the nth Triangular number. Like all pentagonal numbers, it is the sum of the n consecutive numbers starting with n. so the 13th pentagonal number is 13 + 14 + 15 + ... 25 = 247
247 + the product of its digits, 56, is 303, a palindrome.
247 - the product of its digits, 56, is 291, a palindrome.
And the number 66 can be partitioned into squares in 247 different ways.
The 248th Day of the Year
248 is the smallest number (above 1) for which the arithmetic, geometric, and harmonic means of φ(n)(Tne umber of positive integers less than n that are relatively prime to it, 120) and σ(n) (the sum of positive integers less than n that are factors of n, 480) are all integers.
248 = 28 - 23 , which can also be expressed as 2^n - n
248 is the only number such that its unique prime factorization is of the form \(p^{p+1}[p^{p+3}-1]\) *Prime Curios
248 is an untouchable number, there is no number n from which a subset of its divisors sum to 248.
248 is also a refactorable number since it is divisible by the count of its own divisors (8).
Because it is divisible by four and by eight, it is the difference of two squares as (63^2 - 61^2) and (33^2 - 29^2),
The 249th Day of the Year
The 249th day of the year. 249 is the index of a Woodall prime. A Woodall number is a number of the form W(n) = n(2n)-1. The first few are 1, 7, 23, 63, 159, 383, ... (Sloane's A003261). W(249) is prime. [Proof left to the reader, ;-} ] W(2)=7; W(3)=23 and W(6)=383 are all prime. What's the index of the next prime Woodall number? ( named after H. J. Woodall who studied them in 1917)
249 = (3!)3 + (2!)5 + (1!)7 (consecutive odd powers of consecutive factorials) *Derek Orr
and Jim Wilder @wilderlab sent 249 3= 15,438,249 Check 2492n-1 and be surprised, then find out why.
Because 249 is equivalent to \(3 mod_6\) it is the difference of two squares of integers three apart, \(43^2 = 40^2 = 249\). And also the difference of two consecutive squares, 125^2 - 124^2.
249 = 10^2 + 10^2 + 7^2, and also 14^2 + 7^2 + 2^2
Thee first 34 rows of the arithmetic triangle has 259 odd numbers. (How many even?)
249 is two less than a prime, and 249^2 is also two less than a prime. And its cube, which is the 12th Fermat Prime; but alas the fourth power has a factor of 3.
249 is the last year day which can be written as the sum of prime numbers using only the digits 1-5 exactly once in the digits of the prime in only one way: 249 = 241 + 5 + 3: The largest year day that can be written in such a manner in more than one way is a permutation of 249, 294 = 43 + 251 = 53 + 241.
168 and 249 have an interesting relationship, the sum of their digits are equal, and the sum of the squares of their digits are equal. \( 1 + 6 + 8 = 2 + 4 + 9 = 15\) and \(1^2 + 6^2 + 8^2 = 101 = 2^2 + 4^2 + 9^2\)
The 250th Day of the Year
250 is the smallest number expressible as the sum of two positive cubes, which is also expressible as the sum of two (unique) positive squares in more than one way. ( on Feb. 16, 1745 Euler wrote to Goldbach and shows that numbers represented in two different ways as a sum of two squares must be composite; hence 250 is composite. )
53+ 5 3 = 250
152+ 5 2 = 250 ; 13 2 + 92 = 250
250 is only the 18th number that is the sum of two positive cubes
and 250 = (3!)3 + (2!)^5 + (1!)7+ (0!)9 *Derek Orr
Strange that I would learn this from a Brit, but "Length of a baseball pitch, pitcher to batter (18.44 m) is 250 x Diameter of regulation baseball (73.7 mm) *http://www.isthatabignumber.com He used the term for the "pitch" (pitching or bowling area) in cricket, and btw, the cricket pitch is 1 chain, or 22 yards long, and that's 20.12 meters (but the batting (popping) crease is almost 1 1/4 meters in front of the stumps, so the pitching distances are very similar.
250 is the smallest multidigit prime where the sum of the squares of its prime factors is the same as the sum of the squares of its digits. *Prime Curios
250 = 1^2 + 2^2 + 7^2 + 14^2, the sum of the squares of its divisors.
250 is the 49th prime - 1. Its square is also one less than a prime
The 251st Day of the Year
The four consecutive primes 251-257-263-269 all have prime gaps of 6. There are no other consecutive prime gaps for the rest of the year. There have been four primes that had the same prime gap before and after them. There are gaps of six on each side of 53, 157, and 173; and a gap of two on both sides of 5.
251 is a prime number that is also the sum of three consecutive primes (79 + 83 + 89) and of seven consecutive primes (23 + 29 + 31 + 37 + 41 + 43 + 47).
In addition, it is the smallest integer that can be the sum of three cubes in two different ways. 251 =23+ 33+63 = 13+53+53
251 is also the sum of 6 consecutive triangular numbers, 21 + 28 + 36 + 45 + 55 + 66
251 is a cubic automorph since its cube, 15813251, ends in 251.
and there are 251 primes less than 1600.*@MathYearRound
and wow: The 251st Fibonacci number (12776523572924732586037033894655031898659556447352249) has a sum of digits equal to 251. *jim wilder @wilderlab
251 is the 49th Prime, and the largest prime day year that is the concatenation of two squares.
251 = 2^3 + 3^5
All the prime numbers up to 251, without repetition, appear in Benjamin Franklin's original 16-by-16 square. Prime Curios
I found the image here, with lots of notes on additional magic components.
251 is the smallest number that is the sum of three cubes in two ways, 1^3 + 5^3 + 5^3 = 2^3 + 3^3 + 6^3 *Prime Curios
In 1641 Mersenne stated that \(2^251 - 1\) is composite, without proof. Prime Curios (The smallest factor is 503.)
251 can be formed by the difference of two five digit numbers that share no common digit, and thus contain all the digits from 0-9.
40126 - 39875
251 is a palindrome in base 8 (373)
251 is the difference of two consecutive squares, 126^2 - 125^2
251 is a Sophie Germain prime since 2*251+1 is also prime.
The 252nd Day of the Year
The 252nd day of the year; 252 is the smallest number which is the product of two distinct numbers that are reverses of each other: 252 = 12*21 *Number Gossip
(and the next would be?)
252 is a palindrome in base ten, and also in base five 20025 (How many three digit numbers are (non-trivial) palindromes in base ten and one other base less than ten)
If you flip a coin 10 times in a row, there are exactly 252 ways in which it can turn out that you get exactly 5 heads and 5 tails. That is, \( 252 = \binom{10}{5} = \frac{10*9*8*7*6}{5*4*3*2*1} \)
252 = 2^2 x 3^2 x 7. Because it is divisible by four, it is the difference of two squares, 64^2 - 62^2 , but it is also expressible as 24^2 - 18^2 (252/12=21), and 16^2 - 2^2 (252/28 = 9)
252 is divisible by the number of its divisors (18) and is called a refactorable number.
252 is the largest year day that is the sum of the squares of the numbers in a row of Pascal's triangle, the squares of the fifth row are \( 1^2 + 5^2 + 10^2 + 10^2 + 5^2 + 1^1 = 252 \)
and wow: The 251st Fibonacci number (12776523572924732586037033894655031898659556447352249) has a sum of digits equal to 251. *jim wilder @wilderlab
251 is the 49th Prime, and the largest prime day year that is the concatenation of two squares.
251 = 2^3 + 3^5
All the prime numbers up to 251, without repetition, appear in Benjamin Franklin's original 16-by-16 square. Prime Curios
I found the image here, with lots of notes on additional magic components.
251 is the smallest number that is the sum of three cubes in two ways, 1^3 + 5^3 + 5^3 = 2^3 + 3^3 + 6^3 *Prime Curios
In 1641 Mersenne stated that \(2^251 - 1\) is composite, without proof. Prime Curios (The smallest factor is 503.)
251 can be formed by the difference of two five digit numbers that share no common digit, and thus contain all the digits from 0-9.
40126 - 39875
251 is a palindrome in base 8 (373)
251 is the difference of two consecutive squares, 126^2 - 125^2
251 is a Sophie Germain prime since 2*251+1 is also prime.
The 252nd Day of the Year
The 252nd day of the year; 252 is the smallest number which is the product of two distinct numbers that are reverses of each other: 252 = 12*21 *Number Gossip
(and the next would be?)
252 is a palindrome in base ten, and also in base five 20025 (How many three digit numbers are (non-trivial) palindromes in base ten and one other base less than ten)
If you flip a coin 10 times in a row, there are exactly 252 ways in which it can turn out that you get exactly 5 heads and 5 tails. That is, \( 252 = \binom{10}{5} = \frac{10*9*8*7*6}{5*4*3*2*1} \)
252 = 2^2 x 3^2 x 7. Because it is divisible by four, it is the difference of two squares, 64^2 - 62^2 , but it is also expressible as 24^2 - 18^2 (252/12=21), and 16^2 - 2^2 (252/28 = 9)
252 is divisible by the number of its divisors (18) and is called a refactorable number.
252 is the largest year day that is the sum of the squares of the numbers in a row of Pascal's triangle, the squares of the fifth row are \( 1^2 + 5^2 + 10^2 + 10^2 + 5^2 + 1^1 = 252 \)
252 is also a practical number, since every integer smaller than 252 can be formed by adding a subset of the divisors of 252.
252 can be expressed as the sum of prime numbers using only the digits 1-9 once each. 2 + 41 + 59 + 83 + 67. (You can do the same with 225) Clever students will see an alternate way to do 252 manipulating the one above.)
252 is the sum of four cubes (1^3 + 2^3 + 3^3 + 6^3) It can also be expressed as (1^3 + 2^3)(1^3 + 3^3)
The 253rd Day of the Year
253 is the 22nd triangular number, and thus the number of combinations of 23 things taken two at a time. More unusual for a triangular number, it is also the 9th centered heptagonal number. It seems there there are only five known numbers that are both triangular and centered heptagonal. (I found it interesting that if you find the digital roots of the centered hexagonal numbers, the sequence of the digital roots has period 9: repeat[1, 8, 4, 7, 8, 7, 4, 8, 1] (the period is a palindrome))
Although there are 116 semiprimes in the year, 253 is the last semiprime year day that is a triangular number. 253 = 11 x 23, the 22nd triangular number.
Sums of ordered digits of 253 produce triangular numbers, 2 + 5 + 3 = 10, 2 + 53 = 55, 25 + 3 = 28.
253 can be written as the sum of consecutive natural number in three different ways, including 1+2+.... + 22, 18 + 19+... + `28 , and 126+127,
253 is a palindrome in base 12(191)
25-3 is prime. Derek Orr pointed out that 2+53 is also prime, in fact, it’s a Mersenne prime, M7
(Ok, there has to be lots more interesting things about 253, it has all Fibonacci prime digits, so there must be cool stuff out there I'm missing, HELP!?
The 254th day of the Year
254 = 2 x 127
254 is the maximum number of pieces a flat circular pizza could be cut into with n straight lines.... find n. (for help, see bottom of this post, a good quadratic problem)
254 is the average of consecutive primes,
and 254 = 2^8 - 2^1
Probability Fact @ProbFact points out that: Odds of drawing a straight in a 5-card hand: 254 to 1.
254 is a sliding number since 254 = 4 + 250 and 1/4 + 1/250 = 0.254.
254 is the average of consecutive primes,
and 254 = 2^8 - 2^1
Probability Fact @ProbFact points out that: Odds of drawing a straight in a 5-card hand: 254 to 1.
254 is a sliding number since 254 = 4 + 250 and 1/4 + 1/250 = 0.254.
There are only 17 year days that are sliding numbers.
*** the maximal number of pieces in which a pancake, pizza (or a circle) can be divided into by 
linear cuts. They are the bidimensional version of cake numbers.
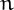linear cuts. They are the bidimensional version of cake numbers.In general,
![\[
p_n = {n+1\choose2}+1 = {n\choose2}+ {n\choose1}+ {n\choose0}=\frac{n^2+n+2}{2}\,.
\]](https://www.numbersaplenty.com/set/pancake_number/pic.3.png)
Pancake numbers are often called lazy caterer numbers, or, more formally, central polygonal numbers.
The 255th Day of the Year
255= 28-2^0 and is the fourth Mersenne number that is not a prime. However it is the product of three distinct Fermat Primes, 3*5*17, and therefore the regular 255-gon is constructible with straightedge and compass. *HT to Don S. McDonald @McDONewt who also pointed out that the next two numbers, 256 and 257 are also constructable since one is a power of two, and the other is a Fermat Prime. John D Cook has a nice overview of Mersene Numbers and Mersene Primes
255 is a also a repdigit in base 2 (11111111) in base 4 (3333), and in base 16 (FF). (What is the next number that is a repdigit in base two and base 4?)
255 = 1 + 2 + 4 + 8 + 16 + 32 + 64 + 128 , Which in binary is the repdigit 11111111
also 255 = 3 + 12 + 48 + 192 (3 + 3x4 + 3x4^2 + 3x4^3) Which in base four is another repdigit, 3333.
255 = 15 + 15x16 , FF in hexdecimal.
233 is a palindrome in base 9 (313) and base 11 (212)
255 is the number of levels on the Pac-Man arcade machine prior to the "kill screen" rendering game over... why 255? (Computer people know )*Jim Wilder@wilderlabIn the 3n+1 or Collatz problem, the sequence for n = 255 reaches higher than any other year day, to the value of 19,682. The previous high value was at 27, when it reached 9232.(The Collatz Problem seems to have deep relationships in number theory, but no one seems to know how to trace them down. A Medus- like problem with a thousand heads that each distract us from their common purpose.
255 = 5^2 + 6^2 + 7^2 + 8^2 + 9^2
255 = 1 + 2 + 4 + 8 + 16 + 32 + 64 + 128 , Which in binary is the repdigit 11111111
also 255 = 3 + 12 + 48 + 192 (3 + 3x4 + 3x4^2 + 3x4^3) Which in base four is another repdigit, 3333
255 is a sef number, there is no number n so that n + the sum of the digits of n = 255.
255 is the difference of consecutive squares, 128^2 - 127^2 . It is also 28^2 - 23^2, and of 44^2 - 41^2. and 16^2 -1^2.
The 256th Day of the Year
256 is the smallest composite to composite power,44.
A student note for fourth powers, They are always the sum of two (I think consecutive) triangular numbers, 2^4 = 6+10 (t(3) + t(4)); 3^4 = 36 + 45 (t(8) + t(9)); 4^4 = 120 + 136 (t(15) + t(16)). There is a pattern in the index of the larger triangular number of each pair.
The 256th Day of the Year
256 is the smallest composite to composite power,44.
A student note for fourth powers, They are always the sum of two (I think consecutive) triangular numbers, 2^4 = 6+10 (t(3) + t(4)); 3^4 = 36 + 45 (t(8) + t(9)); 4^4 = 120 + 136 (t(15) + t(16)). There is a pattern in the index of the larger triangular number of each pair.
256 is also 2^8 and 16^2 (2^8 let's me show off a fancy word for eighth powers, zinzizinzizinzic which essentially means the square of a squared square. More about the term and it's history here.
perfect powers like 2^8 are pretty rare, with 256 being only the 23rd of the year. There will be only four more until years end. (Yes, of course you want to find them!)
Paul Erdos conjectured that no power of 2 is the sum of distinct powers of three.
from jim wilder @ wilderlab √256 = 2 • 5 + 6
The sum of the cubes of the first 256 odd numbers is a perfect number. \( \sum\limits_{i=0}^{255} (2i+1)^3 = 8589869056\) the 6th perfect number. (all perfect numbers (except 6) are the sum of the cubes of first 2n odd cubes for some (but not all) n) (so \( 28 = 1^3 + 3^3\) and \( 496=1^3 + 3^3 + 5^3 + 7^3\) ).
256 is the middle number in a run of three successive numbers which are all constructible regular n-gons. 255= 3*5*17, is the product of distinct Fermat Primes, 256=28 and is a power of two, and 257 is a Fermat Prime. *HT to Don S. McDonald @McDONewt
With so many factors of two, 256 is expressible as the difference of two squares in several ways. 65^2 - 63^2, 34^2 - 30^2, and 16^2 - 0^2
256 is a near perfect number, the sum of its aliquot divisors is 255. All powers of two are near perfect (aliquot sum is n-1) but it seems there are no known number(s) which is abundant by one. *OEIS
256 is one less than a prime (257). It is the eighth power of two, and four of them are one less than a prime, four are not.... but in the long run???
The 257th Day of the Year
The four consecutive primes 251-257-263-269 all have prime gaps of 6. There have been four primes that had the same prime gap before and after them. There are gaps of six on each side of 53, 157, and 173; and gaps of 12 around 211. A triplet of gaps of 2 between 3, 5, & 7,
257 is a prime number of the form 223+1 and therefore a Fermat prime. It is currently the second largest known Fermat prime. It is the only known Fermat Prime that is not part of a Twin Prime pair.
257 is the third consecutive number (255,256,257) for which the regular n-gon is constructible with straightedge and compass. The 255th day of the year; 255= 28-1 is the product of three distinct Fermat Primes, 3*5*17, 256=28 is a power of two, and 257 is a Fermat Prime *HT to Don S. McDonald @McDONewt (Goldbach used the fact that all Fermat Numbers are 2 + product of all smaller Fermat Primes to prove that no two Fermat Numbers share a common prime divisor)
At one time, it was announced that \(2^{257} -1) was prime also, and thus a new perfect number had been found. On March 27,1936 The Associated Press released a story that a new 155 digit perfect number had been found by Dr. S. I. Krieger of Chicago. The number was \(2^{256}(2^{257} - 1)\) by proving the \(2^{257} -1\) was prime. This was shocking since D. H. Lehmer and M. Kraitcik had announced that the number was composite in 1922. Unfortunately, their method did not include giving a factor of the number. The perfection of the number was doubted by most mathematicians, but the actual factoring to prove it was composite didn't happen until 1952 when the SWAC confirmed it was composite by finding a proper divisor. *Beiler, Recreations in the Theory of Numbers.
257 = 44 + 1 It is the largest known prime of the form nn + 1. *Prime Curios 2^2 + 1 is also prime, are there more? <br /><br />
More than 90% of all positive integers are composite numbers that have a lowest prime factor of 257 or less. (Would this be equally true for nearby primes like 251 or 263? It seems like as the prime grows in value, the Pctg would slowly diminish. Yes? No? Teach me.)
2257 - 1 is the largest number in Mersenne's list of primes in the preface to his Cogitata Physica-Mathematica (1644), it later turned out to be Composite. * Dan Garbowitz @DGoneseventh
Ones and zeros, 257 written in different bases, 1000000012, 100014 10116 (Students, Why is eight not in this list?)
257 = 2^8 + 2^0
Prime Curios points out that 257 is the largest of 15 consecutive primes of the form 2T + 1 where T is the triangular numbers. 1, 3, 6, ...
257 is a factor of 1068349. This division problem includes all the digits from 0 - 9 once each.
257 is a palindrome in base 2 with LOTS of zeros, (100000001) and in base 4( 10001) and yes, in base 16 (101)
There is(was?) a Pac-Man themed restaurant called Level 257 located in Schaumburg, Illinois. It is in reference to the kill screen reached in Level 256 in the Pac-Man arcade game. I checked online and in the midst of the Pandemic they are open daily with games, and shortlane bowling (No more gutter balls for this boy!).
More than 90% of all positive integers are composite numbers that have a lowest prime factor of 257 or less. (Would this be equally true for nearby primes like 251 or 263? It seems like as the prime grows in value, the Pctg would slowly diminish. Yes? No? Teach me.)
2257 - 1 is the largest number in Mersenne's list of primes in the preface to his Cogitata Physica-Mathematica (1644), it later turned out to be Composite. * Dan Garbowitz @DGoneseventh
Ones and zeros, 257 written in different bases, 1000000012, 100014 10116 (Students, Why is eight not in this list?)
257 = 2^8 + 2^0
Prime Curios points out that 257 is the largest of 15 consecutive primes of the form 2T + 1 where T is the triangular numbers. 1, 3, 6, ...
257 is a factor of 1068349. This division problem includes all the digits from 0 - 9 once each.
257 is a palindrome in base 2 with LOTS of zeros, (100000001) and in base 4( 10001) and yes, in base 16 (101)
There is(was?) a Pac-Man themed restaurant called Level 257 located in Schaumburg, Illinois. It is in reference to the kill screen reached in Level 256 in the Pac-Man arcade game. I checked online and in the midst of the Pandemic they are open daily with games, and shortlane bowling (No more gutter balls for this boy!).
257 = 5^3 x 2^2 - 3^5 Is it possible to express all primes as A x B +/- C where A, B, and C are each a power of bases 2, 3, and 5 (all distinct)
The 258th Day of the Year
258 is a sphenic(wedge) number (the product of three distinct prime factors..258 = 2·3·43) it is also the sum of four consecutive primes 258 = 59 + 61 + 67 + 71
(Jim Wilder@Wilderlab pointed out that 2,5,&8 are the numbers in the center column of a phone or calculator.) Jim's comment reminded me of a math type phone joke I saw at Wolfram Mathworld: "I'm sorry, the number you have dialed is an imaginary number. Please rotate by 90o and try again." Taking this joke one step further gives the "identity" \( 8*i = \infty \) And that reminds me of this cartoon at Mind Research Institute.
The Number Zoo gives a Magic square using 16 consecutive primes, with a constant of 258
Prime Curios also states that if you take all six permutations of 258, put them in order, and make the 18 digit concatenation of them, it is the composite number between a prime pair. Can you find others like this?
258 is the sum of four consecutive Prime numbers, 59 + 81 + 67 +71 *Wikipedia
258 = 6^3 + 6^2 + 6, or 1110 in base six. Tomorrow that will be 1111.
258 is the sum of two consecutive primes 127 + 131.
and 258 = 2^8 + 2^1.
The 258th Day of the Year
258 is a sphenic(wedge) number (the product of three distinct prime factors..258 = 2·3·43) it is also the sum of four consecutive primes 258 = 59 + 61 + 67 + 71
(Jim Wilder@Wilderlab pointed out that 2,5,&8 are the numbers in the center column of a phone or calculator.) Jim's comment reminded me of a math type phone joke I saw at Wolfram Mathworld: "I'm sorry, the number you have dialed is an imaginary number. Please rotate by 90o and try again." Taking this joke one step further gives the "identity" \( 8*i = \infty \) And that reminds me of this cartoon at Mind Research Institute.
The Number Zoo gives a Magic square using 16 consecutive primes, with a constant of 258
*Prime Curios points out that 258 is the minimum magic sum of a magic square utilizing sixteen consecutive primes. First found by Allan W. Williams, Jr., of Washington, D.C. <
Prime Curios also states that if you take all six permutations of 258, put them in order, and make the 18 digit concatenation of them, it is the composite number between a prime pair. Can you find others like this?
258 is the sum of four consecutive Prime numbers, 59 + 81 + 67 +71 *Wikipedia
258 = 6^3 + 6^2 + 6, or 1110 in base six. Tomorrow that will be 1111.
258 is the sum of two consecutive primes 127 + 131.
and 258 = 2^8 + 2^1.
258 is 47 + the 47th prime, 211
The 259th Day of the Year
259 expressed in base six is a repunit, 1111 (63+62+ 61+60= 216+36+6+1=259). And also in base 36, which we all use often, its 77.
259 can be expressed as the sum of four cubes in two different ways, 259 = 13 + 23 + 53 + 53= 23 + 23 + 33 + 63
and for my ex-students from Japan, 259 is The number of Pokémon originally available in Pokémon Gold and Silver
259 = 7 x 37, and there are seven primes between these two primes.
The 259th Day of the Year
259 expressed in base six is a repunit, 1111 (63+62+ 61+60= 216+36+6+1=259). And also in base 36, which we all use often, its 77.
259 can be expressed as the sum of four cubes in two different ways, 259 = 13 + 23 + 53 + 53= 23 + 23 + 33 + 63
and for my ex-students from Japan, 259 is The number of Pokémon originally available in Pokémon Gold and Silver
259 = 7 x 37, and there are seven primes between these two primes.
Probably 259 is the largest number that can be written in two ways as \(2^x + 3y\). Here \(259 = 2^8 + 3^1 = 2^4 + 3^5\).
And just in case you are dialing long distance to Zanzibar (don't we all do that on occasion) the country code is 259, and you are welcome.
259 is a repunit palindrome in base six (1111). 1 + 1(6) + 1(36) + 1(216)
259 = 125^2 - 124 ^2, but also 22^2 - 15^2.
259 can be divided into two squares whose product is a square, 25 x 9 = 225
The 260th Day of the Year
260 is the constant for each row, column and diagonal of the first known(1891) 8x8 bimagic square. The 8x8 is the smallest order possible for a bimagic square (the squares of the numbers also form a magic square) that uses consecutive digits. The constant for the magic square formed by the squares is 11,180.
260 is also the constant of Benjamin Franklin's 8x8 Magic square.
260 is also the sum of the squares of the divisors of 15. /( 260 = 1^2 + 3^2 + 5^2 + 15^2 /)
260 =66^2-64^2 , and also 16^2 + 2^2 = 4^4 + 4^1, and 14^2 + 8^2
260 is a Palindrome in base 8 (404)
The Mayan Sacred Calendar had a 260 year cycle.
A 5x5 magic square with a constant of 260 can be formed by taking the standard 1-25 magic square and multiplying each term by four. Another is to use 39, 40, 41,... , 64
The 261st Day of the Year
261 = 15^2 + 6^2. It is also 45^2 - 42^2 and 131^2 - 130^2
261 is the number of possible unfolded tesseract patterns. (Charles Howard Hinton coined the term tesseract (4-dimensional "cube"). He is also the inventor of the baseball pitching gun.) (see Baseball and the Fourth Dimension)
If you draw diagonals in a 16 sided polygon, it is possible to dissect it into 7 quadrilaterals. There are 261 unique ways to make this dissection.
261 is the only three digit number n, for which 2^n - n is prime. *Prime Curios
261 is divisible by 9, the sum of its digits, so it is a Joy-Giver (Harshad) number.
261 Fearless, a non-profit organization started by Kathrine Switzer, who in 1967 wore bib number 261 when she became the first woman to run the Boston Marathon as a numbered entrant. *Wikipedia
This should have been the Day of the Year in 2021, as that's the base five representation for 261(2021)
A bracelet with 261 Blue beads and 3 Red beads can be ordered in 261 different ways.
261 = 4^4 + 4^1 + 4^0
The 261st Day of the Year
261 = 15^2 + 6^2. It is also 45^2 - 42^2 and 131^2 - 130^2
261 is the number of possible unfolded tesseract patterns. (Charles Howard Hinton coined the term tesseract (4-dimensional "cube"). He is also the inventor of the baseball pitching gun.) (see Baseball and the Fourth Dimension)
If you draw diagonals in a 16 sided polygon, it is possible to dissect it into 7 quadrilaterals. There are 261 unique ways to make this dissection.
261 is the only three digit number n, for which 2^n - n is prime. *Prime Curios
261 is divisible by 9, the sum of its digits, so it is a Joy-Giver (Harshad) number.
261 Fearless, a non-profit organization started by Kathrine Switzer, who in 1967 wore bib number 261 when she became the first woman to run the Boston Marathon as a numbered entrant. *Wikipedia
This should have been the Day of the Year in 2021, as that's the base five representation for 261(2021)
A bracelet with 261 Blue beads and 3 Red beads can be ordered in 261 different ways.
261 = 4^4 + 4^1 + 4^0
My conjecture: There is no square that is made up of five Pythagorean triangles with a side shorter than 261, as shown *HT to @simon_gregg
The 262nd Day of the Year.
262 is a palindrome, and twice a palindrome (2 x 131)
262 is the 5th meandric number. A meander is a self-avoiding closed curve which intersects a line a number of times. Intuitively, a meander can be viewed as a straight road crossing a river over a number of bridges.[ The term meander is drawn from the Greek name of an actual winding river, the Maiandros.]
2625 begins with the digit 1234543.... novel
262 should be day of the year for 2022, 262 in base five is 2022.
262 is the number of equilateral triangles formed out of matches in a hexagonal chunk with four matchsticks on a side..(Can you find the 38 equilaterals in the hexagon with two matchsticks on a side)
And for those "Wikipedia has everything" fans, the smallest number that does not have its own number page on Wikipedia. And yet, it is still a Happy Number. It takes only four iterations of summing the squares of the digits to get to one.
a Happy Number cartoon from John Golden, an educator well worth following, and close reading.
The 263rd Day of the Year
263 is an irregular prime. (a regular prime is an odd prime which divides the numerator of a Bernoulli Number) They became of great interest after 1850 when Kummer proved that Fermat's Last Theorem was true for any exponent that was a regular prime.
\( 263^2 = 69169 \) A strobogrammatic number (appears the same rotated by 180o. *Prime Curos adds that it is the largest known number for which this is true.
Jim Wilder@wilderlab pointed out also that the length of 263!! (Hate that notation, it is the product of all the odds from 263 down to 1) is 263 digits. Once more pushing for a different and clearer notation. Even Prime Curios \(263!_2\) is better, but doesn't allow for partial descent, so \(n!_{a,b}\) with a as step size, and b as number of steps would allow \(43!_{5, 3} = 43 * 38 * 33 \) And if you changed the lowered text to upper, the 5 could mean count UP.
263 is the sum of five consecutive primes, 263 = 43 + 47 + 53 + 59 + 61 , and the average of the primes on each side of it, \( 263 = \frac{257 + 269}{2} \)
263 is the sum of three primes that are all palindromes, 151 + 101 + 11, ending in the sum of the digits of 263.
In 1919 Ramunjan wrote a new proof of Bertrand's Postulate, which he points out was first stated by Chebyshev, and I always give it in the poetic form I learned it first.
Chebyshev said it
So I'll say it again
There is always a Prime Between n and 2n
Of course Chebyshev actually said between n and 2n-2, but.....
He created a sequence of integers that incremented no more than one as the primes grew. That sequence of Primes, 2, 11, 17, 29, 41.. are called Ramanujan primes, and 263 is one of them. It turns out that there are 24 primes between 263 and 263/2. 131 is the 32nd Prime, 263 is the 56th. Guess Ramanujan got that one right. the smallest number such that if x >= a(n), then pi(x) - pi(x/2) >= n,
263 is an irregular Prime. 1850, Kummer proved that Fermat's Last Theorem is true for a prime exponent p if p is regular. This focused attention on the irregular primes. In 1852, Genocchi was able to prove that the first case of Fermat's Last Theorem is true for an exponent p,
262 is the number of equilateral triangles formed out of matches in a hexagonal chunk with four matchsticks on a side..(Can you find the 38 equilaterals in the hexagon with two matchsticks on a side)
And for those "Wikipedia has everything" fans, the smallest number that does not have its own number page on Wikipedia. And yet, it is still a Happy Number. It takes only four iterations of summing the squares of the digits to get to one.
a Happy Number cartoon from John Golden, an educator well worth following, and close reading.
 |
| *@mathhombre |
The 263rd Day of the Year
263 is an irregular prime. (a regular prime is an odd prime which divides the numerator of a Bernoulli Number) They became of great interest after 1850 when Kummer proved that Fermat's Last Theorem was true for any exponent that was a regular prime.
\( 263^2 = 69169 \) A strobogrammatic number (appears the same rotated by 180o. *Prime Curos adds that it is the largest known number for which this is true.
Jim Wilder@wilderlab pointed out also that the length of 263!! (Hate that notation, it is the product of all the odds from 263 down to 1) is 263 digits. Once more pushing for a different and clearer notation. Even Prime Curios \(263!_2\) is better, but doesn't allow for partial descent, so \(n!_{a,b}\) with a as step size, and b as number of steps would allow \(43!_{5, 3} = 43 * 38 * 33 \) And if you changed the lowered text to upper, the 5 could mean count UP.
263 is the sum of five consecutive primes, 263 = 43 + 47 + 53 + 59 + 61 , and the average of the primes on each side of it, \( 263 = \frac{257 + 269}{2} \)
263 is the sum of three primes that are all palindromes, 151 + 101 + 11, ending in the sum of the digits of 263.
In 1919 Ramunjan wrote a new proof of Bertrand's Postulate, which he points out was first stated by Chebyshev, and I always give it in the poetic form I learned it first.
Chebyshev said it
So I'll say it again
There is always a Prime Between n and 2n
Of course Chebyshev actually said between n and 2n-2, but.....
He created a sequence of integers that incremented no more than one as the primes grew. That sequence of Primes, 2, 11, 17, 29, 41.. are called Ramanujan primes, and 263 is one of them. It turns out that there are 24 primes between 263 and 263/2. 131 is the 32nd Prime, 263 is the 56th. Guess Ramanujan got that one right. the smallest number such that if x >= a(n), then pi(x) - pi(x/2) >= n,
263 is an irregular Prime. 1850, Kummer proved that Fermat's Last Theorem is true for a prime exponent p if p is regular. This focused attention on the irregular primes. In 1852, Genocchi was able to prove that the first case of Fermat's Last Theorem is true for an exponent p,
Srinavasa Raghava pointed out that 2+6+3 is prime, and 2x + 6x + 3x is prime when x = 3, 9, 13, 25, 27 and 29. Wonder what happens if you try that for other three digit numbers? (Don't just sit there children, get checking, and share your results with me if you find something fascinating.)
The 264th Day of the Year
264 = 23x3x11 is a harshad number (a number divisible by the sum of its digits). The word "Harshad" comes from the Sanskrit harṣa (joy) + da (give), meaning joy-giver. The numbers were defined and named by the famous Indian Mathematician D. R. Kaprekar.
Jim Wilder @wilderlab pointed out that the sum of all 2-digit numbers you can make from 264 totals 264... 24 + 42 + 26 + 62 + 46 + 64.
2642 = 69696, a palindrome; and 264 is the sum of ten consecutive primes. *Chaw points out that this is the only square less than 2,000,000,000 that is both a palindrome and a sum of twin primes, 34847 and 34849.
264 is a repdigit in base 11 (222).
264 is a Harshad (Joy-giver) number, divisible by the sum of its digits, 12.
264 = 66^2 - 64^2 = 35^2- 31^2,
264 is one more than a prime.
264 is the Area of two integer sided triangles, with sides 33, 34, 65 and 44, 37, 15.
264 = 2^8 + 2^3,
The 265th Day of the Year
265 is !6 (sub-factorial 6), the number of ways that six ordered objects can be mis-ordered so that each is in the wrong spot. See Subfactorial
The term "subfactorial "was introduced by Whitworth (1867 or 1878; Cajori 1993, p. 77). Euler (1809) calculated the first ten terms. For example, the only derangements of {1,2,3} are {2,3,1} and {3,1,2}, so !3=2 (Pssst, students... You can find !n by dividing n! by e, and rounding to nearest integer)
265 is the sum of two squares in two different ways, including one that is the sum of consecutive squares. \(265 = 3^2 + 16^2 = 11^2 + 12^2 \)
2652 is also the sum of two squares in two different ways, making 265 the hypotenuse of two Pythagorean Triangles. One of them is 23, 264, 265.
265 = 16^2 + 3^2 and 29^2 - 24^2,
265 = !6 or subfactorial 6 The number of ways of putting six letters into six addressed envelopes so that each is mis-addressed.
265 is a semi-prime, 5 x 53. The sum of the digits of 265 is the same as the sum of the digits of its factors, sometimes called Joke numbers.
To form a 5x5 magic square with a constant of 265, take the standard 5x5 using 1-25, and add forty to each term. You can also multiply all the digits from 1-25 by four, then add one, using the numbers 5, 9, 13,....., 101
*Hat Tip to Srinivasa Ragahava
The 266th Day of the Year
266 can be expressed as 222 in base 11.
266 is the sum of four cubes, \(266 = 2^3 + 2^3 + 5^3 + 5^3 \)
It is also the index of the largest proper subgroups of the sporadic group known as the Janko group J1
266 has a digit sum of 12, a divisor of 266, so it is a Joy-Giver number.
The sum of the divisors of 266 is 18^2 = 324.
The 266th Day of the Year
266 can be expressed as 222 in base 11.
266 is the sum of four cubes, \(266 = 2^3 + 2^3 + 5^3 + 5^3 \)
It is also the index of the largest proper subgroups of the sporadic group known as the Janko group J1
266 has a digit sum of 12, a divisor of 266, so it is a Joy-Giver number.
The sum of the divisors of 266 is 18^2 = 324.
266 is the sum of five consecutive Triangular numbers. 15 + 21 + 28 + 36 + 45 + 55 + 66. On Sept , 1796 Gauss's entry "EγPHKA! num=Δ+Δ+Δ" in his scientific diary, recording his discovery that every positive integer is the sum of (at most) three triangular numbers. Can you find three for 266? Can you find three or less in more than one way?
Many people know that N! has N digits for N= 22, 23, and 24. Surprisingly, to me, there are also three consecutive numbers for which N! has 2N digits, 266, 267, and 268. For N! has 3N digits, only two consecutive numbers, 2712 and 2713.For N! having 4N digits, there are again two consecutive occurrences, 27175 and 27176. For 5N we go back to three consecutive digits, 271819, 271820, 271821 Note the increase by a power of ten as a limit, and the higher you go, the closer they approach e * 10^n. It has been conjectured that there are always at two or three consecutive numbers for every digit, but never more. The first 100 such numbers are found at A058814 - OEIS Thanks to Derek Orr and Frank Kampas for some help and direction on this.
This is the 267th Day of the Year
267 = 46^2 - 43^2, and also 134^2 - 133^2
267 is the smallest number n such that n+ a googol is prime. (anyone want to find the next one? A quick mental problem for students, How do you know that 269+Googol will not be prime?))
267 can be written as the sum of five cubes in two ways, \( 267 = 1^3 + 2^3 + 2^3 + 5^3 + 5^3 = 2^3 + 2^3 + 2^3 + 3^3 + 6^3 \)
Gauss proved that all numbers are the sum of, at most, three triangular numbers. (see July 10, events 1796) Can you find three triangular numbers that sum to 267?, can you find a sum with two? How many can you find in two or less?
Many people know that N! has N digits for N= 22, 23, and 24. Surprisingly, to me, there are also three consecutive numbers for which N! has 2N digits, 266, 267, and 268.
The 268th Day of the Year.
268 is the smallest number whose product of digits is 6 times the sum of its digits. (A good classroom exploration might be to find numbers in which the product of the digits is n x the sum of the digits for various values of n.. more generally, for what percentage of numbers is the sum a factor of the product at all?)
268 is the sum of two consecutive primes, 268 = 131 + 137
268 is divisible by 4, and is therefore expressible as the difference of two squares, 68^2 - 66^2
Prime Curios offers this little mental conversion, 268 inches of 1/8 inch copper wire weighs 1 pound. There is no AWG standard gauge wire that is 1/8 of an inch diameter, but AWG 8 is really close. For students, what would a similar length of 1/4 inch diameter copper wire weigh?
The two odd numbers adjacent to 6*268 form a pair of twin primes, and the next two odd numbers after 268 are a pair of twin primes. And the 268th prime, is the smaller of a pair of twin primes.
And 268 is a Palindrome in base 8 (414)
The 268th Day of the Year.
268 is the smallest number whose product of digits is 6 times the sum of its digits. (A good classroom exploration might be to find numbers in which the product of the digits is n x the sum of the digits for various values of n.. more generally, for what percentage of numbers is the sum a factor of the product at all?)
268 is the sum of two consecutive primes, 268 = 131 + 137
268 is divisible by 4, and is therefore expressible as the difference of two squares, 68^2 - 66^2
Prime Curios offers this little mental conversion, 268 inches of 1/8 inch copper wire weighs 1 pound. There is no AWG standard gauge wire that is 1/8 of an inch diameter, but AWG 8 is really close. For students, what would a similar length of 1/4 inch diameter copper wire weigh?
The two odd numbers adjacent to 6*268 form a pair of twin primes, and the next two odd numbers after 268 are a pair of twin primes. And the 268th prime, is the smaller of a pair of twin primes.
And 268 is a Palindrome in base 8 (414)
Many people know that N! has N digits for N= 22, 23, and 24. Surprisingly, to me, there are also three consecutive numbers for which N! has 2N digits, 266, 267, and 268. 268 is the last year date that appears in this sequence. See 266 for a link and more information.
The 269th Day of the Year
(on non-leap years, the 269th day is Sep 26, and the date is written 26/9 in much of Europe. This is the only day of the year which presents itself in this way. (Are there any days that work using month/day?)
269 is a regular prime, an Eisenstein prime with no imaginary part, a long prime, a Chen prime, a Pillai prime, a Pythagorean prime, a twin prime, a sexy prime, a Higgs prime, a strong prime, and a highly cototient number. So many new terms to look up... Well? Look them up.
269 is the smallest natural number that cannot be represented as the determinant of a 10 × 10 (0,1)-matrix
Prime Curios offers this interesting convention of prime numbers, "The longest official game of chess on record (269 moves) took place in Yugoslavia on 2/17/89 and ended in a draw. Note that 2, 17, 89, and 269 are all prime numbers." And I'm guessing that Yugoslavia was a Prime country in its day.
Prime Curios also had this interesting tidbit, "The smallest prime whose square, 72361, is a concatenation of primes in two ways, i.e., (7, 23, 61) and (7, 2, 3, 61).)
269 is the largest prime factor of 9! + 1 = 362881.
269 Like all Pythagorean Primes (of the form 4n+1) are the sum of two squares, conjectured by Fermat, proved by Euler. 269 = 10^2 + 13^2.
269 is also the Hypotenuse of a Primitive Pythagorean triple, (69, 260 269)
269 is also the difference of two squares, as 135^2 - 134^2,
The 270th Day of the Year
the harmonic mean of the factors of 270 is an integer. The first three numbers with this property are 1, 6, and 28 (which are all perfect #s).. what is the next one? Often called harmonic numbers, they are sometimes called Ore numbers for Øystein Ore, who studied them, and showed that all perfect #s are harmonic. . Many of them also have the arithmetic mean of their divisors is an integer, but not all.
270 is the sum of eight consecutive primes, 270 = 19 + 23 + 29 + 31 + 37 + 41 + 43 + 47 ; and the sum of three cubes \(270 = 3^3+ 3^3 + 6^3 \).
10! = 3628800 has 270 factors. (A really good high school student should be able to confirm this quickly.)
270, with a digit root of nine, and a digit sum of nine, is divisible by the sum of its digits and thus, a Joy-Giver (Harshad) number.
270 is also the smallest positive integer with divisors ending in each of the digits 1- 9, divisible by 1, 2, 3, 54, 5, 6, 27, 18 ,9,.
and of course, between a pair of twin primes, it is the average of two primes.
270 has only three prime factors, the consecutive primes 2, 3, and 5.
The 269th Day of the Year
(on non-leap years, the 269th day is Sep 26, and the date is written 26/9 in much of Europe. This is the only day of the year which presents itself in this way. (Are there any days that work using month/day?)
269 is a regular prime, an Eisenstein prime with no imaginary part, a long prime, a Chen prime, a Pillai prime, a Pythagorean prime, a twin prime, a sexy prime, a Higgs prime, a strong prime, and a highly cototient number. So many new terms to look up... Well? Look them up.
269 is the smallest natural number that cannot be represented as the determinant of a 10 × 10 (0,1)-matrix
Prime Curios offers this interesting convention of prime numbers, "The longest official game of chess on record (269 moves) took place in Yugoslavia on 2/17/89 and ended in a draw. Note that 2, 17, 89, and 269 are all prime numbers." And I'm guessing that Yugoslavia was a Prime country in its day.
Prime Curios also had this interesting tidbit, "The smallest prime whose square, 72361, is a concatenation of primes in two ways, i.e., (7, 23, 61) and (7, 2, 3, 61).)
269 is the largest prime factor of 9! + 1 = 362881.
269 Like all Pythagorean Primes (of the form 4n+1) are the sum of two squares, conjectured by Fermat, proved by Euler. 269 = 10^2 + 13^2.
269 is also the Hypotenuse of a Primitive Pythagorean triple, (69, 260 269)
269 is also the difference of two squares, as 135^2 - 134^2,
The 270th Day of the Year
the harmonic mean of the factors of 270 is an integer. The first three numbers with this property are 1, 6, and 28 (which are all perfect #s).. what is the next one? Often called harmonic numbers, they are sometimes called Ore numbers for Øystein Ore, who studied them, and showed that all perfect #s are harmonic. . Many of them also have the arithmetic mean of their divisors is an integer, but not all.
270 is the sum of eight consecutive primes, 270 = 19 + 23 + 29 + 31 + 37 + 41 + 43 + 47 ; and the sum of three cubes \(270 = 3^3+ 3^3 + 6^3 \).
10! = 3628800 has 270 factors. (A really good high school student should be able to confirm this quickly.)
270, with a digit root of nine, and a digit sum of nine, is divisible by the sum of its digits and thus, a Joy-Giver (Harshad) number.
270 is also the smallest positive integer with divisors ending in each of the digits 1- 9, divisible by 1, 2, 3, 54, 5, 6, 27, 18 ,9,.
and of course, between a pair of twin primes, it is the average of two primes.
270 has only three prime factors, the consecutive primes 2, 3, and 5.
270 is the fifth, and largest year day which has an integral Harmonic mean for the divisors (including n) of the number. These are usually called Harmonic Divisor numbers to distinguish them from the Harmonic numbers (they are sometimes called Ore numbers after Oystein Orr). All perfect numbers have this property, 6 and 28 for example, and my experience is that all perfect numbers have a HM which is prime but the converse is not true. The harmonic mean of the divisors of 270 is six, but the harmonic mean of 140 is 5, the same as the harmonic mean of the divisors of 496, the next perfect number after 28. The first five perfect numbers have harmonic means of their divisors of 2, 3, 5, 7, and 13. The harmonic mean of the divisors of a perfect number is the index of the Mersenne prime which is a factor of the number , 496 = \(2^4 x (2^5 - 1) \) and the harmonic mean of its divisors is 5.
No comments:
Post a Comment