In 1657, Fermat challenged the mathematicians of Europe and England, "We await these solutions, which, if England or Belgic or Celtic Gaul do not produce, then Narbonese Gaul (Fermat's region) will." Among the challenges was this 500-year-old example from Bhaskara II: x2 - 61y2 = 1 (x, y > 0). *Prime Curios
Among all the primes less than 10^9, the final two digits most common is 61.
As a prime number of the form 4n+1, 61 can be written as the sum of two squares in only one way, 5^2+6^2 .
61# (read 61 primorial, the product of 61 and all lesser primes) is the smallest Primorial that is Pandigital (Contains all the numerals 0-9). Guess you could say it is the most Petite Primorial Pandigital.
If you multiply 61 by its digit reversal, 16, and then add one, you get a prime. The smallest multidigit prime for which this is true.
The smallest prime that can be written as the sum of a prime number of primes to prime powers in a prime number of ways: \(2^2 + 2^3 + 7^2\), \(2^2 + 5^2 + 2^5\), and \(3^2 + 5^2 + 3^3\).*Prime Curios
If you divide 61! by 16! and add one, you get a prime number which has a prime number of digits and a prime sum of its digits. If instead you multiply them, and subtract 1, you get another prime with a prime sum of digits. *Prime Curios
And if you start searching pi at the 61st digit after the decimal point, you will find a string of all ten distinct numerals.
The reciprocal of 61 has a repeating decimal of length 60. 1/61 = 0.016393442622950819672131147540983606557377049180327868852459... Primes, p, with reciprocals of length p-1; have the unique property that the first n/2 digits have a 9's compliment in the same position of the next n/2 digits (for a simple example, 1/7 = .142857.. and 1+8 = 4+5 = 2+7 = 9 ) Joshua Zucker corrected me for calling this "unique", as there are other primes with periods less than n-1 that share this property of compliments, 1/13 for example. By the way, that reciprocal is the smallest prime with the same equal numbers of all ten numerals.
If you take the five consecutive primes from 61 to 79, and arrange them in a 3x3 square matrix, then the rows and columns sum to three more consecutive primes ( 199, 211, 223) *Prime Curios
 |
| *Prime Curios |
If A=1,... Z=26, then the word PRIME is prime. (P+R+I+M+E --> 16+18+9+13+5 =61 61 is the exponent of the 9th Mersenne prime.(261 − 1 = 2,305,843,009,213,693,951) (But amazingly, somehow Mersenne omitted this exponent in his list of conjectured primes.
Sixty-one has no repeat letters, and if you spell out any larger prime in English, you will never find another with no repeated letters.
61 is also a Keith number, because it recurs in a Fibonacci-like sequence started from its base 10 digits: 6, 1, 7, 8, 15, 23, 38, 61.. (Keith numbers were introduced by Mike Keith in 1987 who called them repfigit number, short for repetitive Fibonacci-like digit). They are computationally very challenging to find, with only about 100 known.)
AND the 61st Fibonacci number, is the first Pandigital Fibonacci Number, 2504730781961.
AND no odd Fibonacci number is divisible by 61.
On June 30, of 2012, a Leap Second was added to the clock, and created a minute with 61 seconds.
The 62nd Day of the Year:
62 is the smallest number that can be written as the sum of 3 distinct squares in 2 ways. (Students might try to find the smallest number that can be written as the sum of 2 distinct squares in 2 ways)
In base 10, 62 is also the only number whose cube (238328) consists of 3 digits each occurring 2 times
The prime factorization of 62 is 2*31. There are only two numbers whose prime factorization uses only the first three counting numbers once each in its digits. The other is its digit reversal, 26 = 2*13
If you average the first n digits of pi after the decimal point, sometimes the average is an integer (for example, 1+4+1 = 6 and 6/3 = 2 so the first three digits work). 62 digits is the highest known number of digits that work. There is actually a good reason for this, the digits of pi are essentially random, and so they would average 4.5 in the long run. While small numbers may vary more from this value, eventually the values will approach 4.5 within a boundary of less than 1/2, so no integers.
62 is the largest known even number that cannot be expressed as the sum of two odd semiprimes. The sum of the prime factors of this semiprime, 62, gives the largest known number that cannot be expressed as the sum of any two semiprimes.
The digits 62 occur at the 61st & 62nd digits of phi, φ; AND The 61st & 62nd digits of e.
Jim Wilder pointed out a strange amicable relation ship involving 62, 69 and their squares:
\$ 62^2 + 05^2 = 3869\$ but then
\$ 38^2 + 69^2 - 6205\$
speaking of \(62^2\) Any number that ends in 62 will have a square ending in 44. The only numbers whose squares end in double numbers must end in 12, 38, 62, or 88, and they all end in 44. (OK, 38 ends in triple 4)
and 62 is supposedly the age at which Aristotle died.
If you start at the beginning of Pi3.14... the 62nd digit begins a string of all ten distinct numerals.62 in base ten is a repdigit in bases 5 (2225)
And if you ever want to visit Possum Trot, Ky, just get on US 62, and watch for the sign... but don't blink.
62 + the 62nd prime is 355. This is the jargest year day for which this is true.
The 63rd Day of the Year:
in Roman Numerals 63 is LXIII. If you represent each of these letters by its number in the English alphabet you get 12+24+9+9+9=63. (There is one more number that has this quality.)
At right, in honor of my many students from Misawa, Aomorishi, Japan, is Print 63 of Utagawa Hiroshige's 100 views of Edo (Koi No Bori)
\( \phi(63) = 36\) The number of positive integers which are less than 63 and relatively prime to it.
63 can be expressed as powers of its digits, \( 6^2 + 3^3 = 63\)
63 is the Fourth Woodall Number. Numbers of the form n*2<sup>n</sup>-1. 63 = 4*2,sup>4</sup> -1 Woodall Numbers were used in the study of testing prime numbers. There is only one more Woodall Number that is a Day of the Year.
The Five Factorials Game, 2! * 5! / 3! + 4! - 1! = 63
63 is the smallest whole number that can be divided by any number from 1 to 9 without repeating decimals. (What's Next?)
The 64th Day of the Year:
64 is the smallest power of two with no prime neighbor. (What is next value of 2n with no prime neighbor?)
64 is also the first whole number that is both a perfect square and a perfect cube.
The sixth Fermat Prime, 2^64 +1 was factored by F. Landry in 1880 as the product of 274177 and 67280421310721. The next Fermat Prime would not be factored until 1970.
There were 64 disks in Eduard Lucas' myth about the Towers of Hanoi. 64 is also the number of hexagrams in the I Ching, and the number of sexual positions in the Kama Sutra. (I draw no conclusions about that information)
64 can be expressed as the sum of primes using the first four natural numbers once each, 41 + 23 = 64.
There are 64 ordered permutations of nonempty subsets of {1,..., 4}: Eighteenth- and nineteenth-century combinatorialists call this the number of (nonnull) "variations" of 4 distinct objects.
64 is the smallest number with exactly seven divisors.
64 is the smallest square that creates two primes if concatenated with its previous and next squares, i.e., 6449, 6481.*Prime Curios
64 is also the smallest square without a prime neighbor.
64 is a superperfect number—a number such that σ(σ(n)) = 2n. The sum of the divisors (including itself) of 64 is 127, and the sum of the divisors of 127, 1 and 127, add up to 128= 2*64. It is the last Year Day that is Super-Perfect.
And I was told that 64 is the maximum number of strokes used in a Kanji character.
Primes of the form 4n+1 can always be formed as the sum of two integer squares. Primes can only be expressed as such a sum in one way. Since 65 is a semiprime number with two 4n+1 Fermat Prime factors, it can be expressed as the sum of two squares in two ways. 8^2 + 1^2 = 65 = 7^2 + 4^2.
And \( 65 = 1^5 + 2^4 + 3^3 + 4^2 + 5^1 \) *jim wilder @wilderlab
OR, \(65= 0^2 + 1^4 + 2^5 + 3^3 + 4^1 + 5^0 \) *@Expert_says
65 is the constant of a 5x5 normal magic square.
A magic square with the integers 1 through 25 has a sum of 65 in each row, column, and major diagonal.
Euler found 65 integers, which he called "numeri idonei," that could be used to prove the primality of certain numbers.[idoneal numbers (also called suitable numbers or convenient numbers) are the positive integers D such that any integer expressible in only one way as \(x^2 ± Dy^2\) (where x2 is relatively prime to Dy2) is a prime, prime power, twice one of these, or a power of 2. In particular, a number that has two distinct representations as a sum of two squares (such as 65) is composite. Every idoneal number generates a set containing infinitely many primes and missing infinitely many other primes.]
The Five Factorials Game, 2! * 5! / 3! + 4! + 1! = 65
65 is the difference of fourth powers of two consecutive primes. And a note about fourth powers of primes. For any prime greater than five, the last digits of a p^4 either ends in an odd digit followed by six, or an even digit follwed by one.
65 = 15 + 24 + 33 + 42 + 51.
The 66th Day of the Year:
there are 66 different 8-polyiamonds (A generalization of the polyominoes using a collection of equal-sized equilateral triangles (instead of squares) arranged with coincident sides.)
Route 66, known as the Main Street of America was dubbed the "Mother Road" by novelist John Steinbeck, The strobogrammatic partner of 66 is 99, and the Former US 99 was dubbed the "Mother Road" of California during the dust bowl era.
66 is the smallest strobogrammatic number that shares a strobogrammatic factor with its partner, 99.
66 is the smallest number where the sum of its divisors is a perfect square. \(1 + 2 + 3 + 6 + 11 + 22 + 33 + 66 = 12^2 = 144\) There are only three year dates (to my knowledge) for which the sum of the divisors is a square. They all three occur in this MathFacts page, 66, 70, and 81. 66 and 70 even have the same total.
If you wrote out all the numbers on a 12 hour clock, (HrMin, so 6:03 would be 603, etc.), there would be 66 of them that are prime.
The smallest number that can be expressed as a sum of two two-digit primes, each ending with the digit three, in two different ways (66 = 13 + 53 = 23 + 43) and the smallest number that can be expressed as the sum of two primes in six different ways.
66 is the largest day number of the year which does not have a letter "e" in its English spelling. Sixty-six is the 19th such numbers in the year, but the next number without an "e" is 2000.
6 is a triangular number, and 66 is as well, and, Oh Heck Yeah, 666 is too.... And they are all palindromes as well, but 66 is the eleventh triangular number, the only one of these with a palindrome index. (note 6666 is not a triangular number, but 66066 is and it is the 363 triangular number, so its index is a palindrome as well. Only six triangular numbers less than \(10^10\) are palindromes with a palindrome index.)
The 63rd Day of the Year:
in Roman Numerals 63 is LXIII. If you represent each of these letters by its number in the English alphabet you get 12+24+9+9+9=63. (There is one more number that has this quality.)At right, in honor of my many students from Misawa, Aomorishi, Japan, is Print 63 of Utagawa Hiroshige's 100 views of Edo (Koi No Bori)
\( \phi(63) = 36\) The number of positive integers which are less than 63 and relatively prime to it.
63 can be expressed as powers of its digits, \( 6^2 + 3^3 = 63\)
63 is the Fourth Woodall Number. Numbers of the form n*2<sup>n</sup>-1. 63 = 4*2,sup>4</sup> -1 Woodall Numbers were used in the study of testing prime numbers. There is only one more Woodall Number that is a Day of the Year.
The Five Factorials Game, 2! * 5! / 3! + 4! - 1! = 63
63 is the smallest whole number that can be divided by any number from 1 to 9 without repeating decimals. (What's Next?)
The 64th Day of the Year:
64 is the smallest power of two with no prime neighbor. (What is next value of 2n with no prime neighbor?)
64 is also the first whole number that is both a perfect square and a perfect cube.
The sixth Fermat Prime, 2^64 +1 was factored by F. Landry in 1880 as the product of 274177 and 67280421310721. The next Fermat Prime would not be factored until 1970.
There were 64 disks in Eduard Lucas' myth about the Towers of Hanoi. 64 is also the number of hexagrams in the I Ching, and the number of sexual positions in the Kama Sutra. (I draw no conclusions about that information)
64 can be expressed as the sum of primes using the first four natural numbers once each, 41 + 23 = 64.
It can also be done to its reversal 46 = 41 + 3 + 2
There are 64 ordered permutations of nonempty subsets of {1,..., 4}: Eighteenth- and nineteenth-century combinatorialists call this the number of (nonnull) "variations" of 4 distinct objects.
64 is the smallest number with exactly seven divisors.
64 is the smallest square that creates two primes if concatenated with its previous and next squares, i.e., 6449, 6481.*Prime Curios
64 is also the smallest square without a prime neighbor.
64 is a superperfect number—a number such that σ(σ(n)) = 2n. The sum of the divisors (including itself) of 64 is 127, and the sum of the divisors of 127, 1 and 127, add up to 128= 2*64. It is the last Year Day that is Super-Perfect.
And I was told that 64 is the maximum number of strokes used in a Kanji character.
Most mathematicians know the story of 1729, the taxicab number which Ramanujan recognized as a cube that was one more than the sum of two cubes, or the smallest number that could be expressed as the sum of two cubes in two different ways. But not many know that 103 is part of the second such \(64^3 + 94^3 = 103^3 + 1^3 \)
The 65th Day of the Year:
65 is the smallest hypotenuse of two different primitive Pythagorean triangles (and of two other triangles that are not primitive) with all integral sides. (Don't just sit there, find them!) 65 is a 4n+1 semiprime that is factorable into a pair of 4n+1 primes.
The 65th Day of the Year:
65 is the smallest hypotenuse of two different primitive Pythagorean triangles (and of two other triangles that are not primitive) with all integral sides. (Don't just sit there, find them!) 65 is a 4n+1 semiprime that is factorable into a pair of 4n+1 primes.
John Golden @mathhombr found them all, he made a beautiful graphic of them.
Primes of the form 4n+1 can always be formed as the sum of two integer squares. Primes can only be expressed as such a sum in one way. Since 65 is a semiprime number with two 4n+1 Fermat Prime factors, it can be expressed as the sum of two squares in two ways. 8^2 + 1^2 = 65 = 7^2 + 4^2.
And \( 65 = 1^5 + 2^4 + 3^3 + 4^2 + 5^1 \) *jim wilder @wilderlab
OR, \(65= 0^2 + 1^4 + 2^5 + 3^3 + 4^1 + 5^0 \) *@Expert_says
65 is the constant of a 5x5 normal magic square.
A magic square with the integers 1 through 25 has a sum of 65 in each row, column, and major diagonal.Euler found 65 integers, which he called "numeri idonei," that could be used to prove the primality of certain numbers.[idoneal numbers (also called suitable numbers or convenient numbers) are the positive integers D such that any integer expressible in only one way as \(x^2 ± Dy^2\) (where x2 is relatively prime to Dy2) is a prime, prime power, twice one of these, or a power of 2. In particular, a number that has two distinct representations as a sum of two squares (such as 65) is composite. Every idoneal number generates a set containing infinitely many primes and missing infinitely many other primes.]
The Five Factorials Game, 2! * 5! / 3! + 4! + 1! = 65
65 is the difference of fourth powers of two consecutive primes. And a note about fourth powers of primes. For any prime greater than five, the last digits of a p^4 either ends in an odd digit followed by six, or an even digit follwed by one.
65 = 15 + 24 + 33 + 42 + 51.
The 66th Day of the Year:
there are 66 different 8-polyiamonds (A generalization of the polyominoes using a collection of equal-sized equilateral triangles (instead of squares) arranged with coincident sides.)Route 66, known as the Main Street of America was dubbed the "Mother Road" by novelist John Steinbeck, The strobogrammatic partner of 66 is 99, and the Former US 99 was dubbed the "Mother Road" of California during the dust bowl era.
66 is the smallest strobogrammatic number that shares a strobogrammatic factor with its partner, 99.
66 is the smallest number where the sum of its divisors is a perfect square. \(1 + 2 + 3 + 6 + 11 + 22 + 33 + 66 = 12^2 = 144\) There are only three year dates (to my knowledge) for which the sum of the divisors is a square. They all three occur in this MathFacts page, 66, 70, and 81. 66 and 70 even have the same total.
If you wrote out all the numbers on a 12 hour clock, (HrMin, so 6:03 would be 603, etc.), there would be 66 of them that are prime.
The smallest number that can be expressed as a sum of two two-digit primes, each ending with the digit three, in two different ways (66 = 13 + 53 = 23 + 43) and the smallest number that can be expressed as the sum of two primes in six different ways.
66 is the largest day number of the year which does not have a letter "e" in its English spelling. Sixty-six is the 19th such numbers in the year, but the next number without an "e" is 2000.
66 however is not the sum of two squares.
To check if an arbitrary number is the sum of two squares, factor it. If any factor p^a + 1 is divisible by four, then it is not a sum of two positive squares. For 66 = 2 x 3 x 11, the factor of three (or 11) is the killer since one more than either is divisible by four.
6 is a triangular number, and 66 is as well, and, Oh Heck Yeah, 666 is too.... And they are all palindromes as well, but 66 is the eleventh triangular number, the only one of these with a palindrome index. (note 6666 is not a triangular number, but 66066 is and it is the 363 triangular number, so its index is a palindrome as well. Only six triangular numbers less than \(10^10\) are palindromes with a palindrome index.)
And like all triangular numbers, 8 x T + 1 is a square number. For 6, 66, and 666 the squares produced are 7^2, 23^2, and 73^2.
Sixty Six is an unincorporated community in Orangeburg County, South Carolina, United States. Sixty Six is located along U.S. Route 21, north of Branchville.
The 67th Day of the Year:
67 is the largest prime which is not the sum of distinct squares.
Mersenne thought 2^67 - 1 was prime.; In 1867 Lucas proved that it was not prime, but could not find the factors. It was not until October 31, 1903 that Frank Nelson Cole found the factors. ;During Cole's so-called "lecture", he approached the chalkboard and in complete silence proceeded to calculate the value of M67 with the result being 147,573,952,589,676,412,927. Cole then moved to the other side of the board and wrote 193,707,721 × 761,838,257,287, and worked through the tedious calculations by hand. Upon completing the multiplication and demonstrating that the result equaled M67 Cole returned to his seat, not having uttered a word during the hour-long presentation. His audience greeted the presentation with a standing ovation. Cole later admitted that finding the factors had taken "three years of Sundays." *Wik
It is the 19th prime number and the sum of five consecutive primes ending in 19 (7 + 11 + 13 + 17 + 19)
The maximum number of internal pieces possible if a circle is cut with eleven lines. These are sometimes called "lazy caterer's numbers." \( 67 = \binom{11}{0} + \binom {11} {1} + \binom {11}{2} \)
67 is also the smallest prime which contains all ten digits when raised to the tenth power. *Prime Curios
67^10 =1822837804551761449
67 in Roman Numerals if LXVII. If you evaluate that using the a=1, b=2 method, the sum LXVII = 76, the reversal of the digits of 67.
67 is the largest known prime for which 2^p does not contain any zeros.
and Jim Wilder @wilderlab sent 67 = 26 + 21+ 20 = 26 + 21 + 20 = 67
and @expert_says added several more. Students might be shown one relationship, and encouraged to discover others:
67=1² + 1² + 1⁷ + 2⁶ =12+12+17+26
67=1² + 1³ + 1⁶ + 2⁶ =12+13+16+26
67=1² + 1⁴ + 1⁵ + 2⁶= 12+14+15+26
67=1³ + 1³ + 1⁵ + 2⁶=13+13+15+26
67=1³ + 1⁴ + 1⁴ + 2⁶=13+14+14+26
And one smoot is equal to 67 inches.
Foucault's Famous Pendulum had a length of 67 meters. You can see it now in the Beautiful Museum of Arts and Crafts.
67 is palindromic in the consecutive bases 5 (2325) and 6 (1516).
The 68th Day of the Year:
if you searched through pi for all the two digit numbers, the last one you would find is 68. The string 68 begins at position 605 counting from the first digit after the decimal point. (What is the last single digit numeral to appear? One might wonder how far out the string would you have to go to find all possible three digit numbers? )
68 is the largest known number to be the sum of two primes in exactly two different ways:
68=7+61=31+37. All higher even numbers that have been checked are the sum of three or more pairs of primes
68 is a stobogrammatic number, rotated it is 89. Some consider only invertible numbers (rotated they form the same value, like 181) as strobograms. HT to Paul O'Malley By the way, it's the smallest composite number with a prime strobogrammatic partner.
There are exactly 68 ten digit binary numbers in which each digit is the same as one of it's adjacent digits.
68 is the smallest composite number that can be read as a prime number when it is rotated 180o HT Jim Wilder @wilderlab.
And a historical oddity, in 46 BCE, as a result of Julius Caesar's Calendar adjustment, there were 68 days inserted between November and December.
68 is also a Happy number since 68 → 6^2 + 8^2 = 100 → 1^2 + 0^2 + 0^2 = 1
\( 2^68\) is the smallest power of two that is pandigital, with all ten decimal digits. It is a number 21 digits long. *@Fermat's Library
The 69th Day of the Year:
the square and the cube of 69 together contain all ten numerals. 692 = 4761, 693 =328509
1069+69 is prime and; 10069-69 is prime
On Many scientific calculators, 69! is the largest factorial that can be calculated, with an overflow error for larger numbers. 69! is appx 1.711 (1098)
Don S. McDonald @McDONewt pointed out that \( \binom{69}{5}\) = 11238513, 7 Fibonacci #'s almost in order.
69 is a strobogrammatic pair with itself. It is the smallest such number with distinct numbers. Reversing the order of its digits gives 96, another strobogrammatic self-pair. And for a bonus, the sum of the divisors of 69 is 96.
The first squared square to be found was a square filled with 69 different smaller squares. ( electrical network theory was used to make the discovery, previously most mathematicians felt that were not likely to be any squared squares see Jan 21).. The first squared square was published in 1938 by Roland Sprague who found a solution using several copies of various squared rectangles and produced a squared square with 55 squares, and side lengths of 4205
No squared square can be made with less than 21 squares(shown below)
Jim Wilder sent me these facts involving, among others, the number 69.
73 is the largest prime day of the year so that you can append another digit and make another prime six times, 73, 739, 7393, 73939, 739391, 7393913, and 73939133.
73 is the smallest prime that can be expressed as the sum of three cubes, 1^3 + 2^3 + 4^3 =73
The prime number 73 is the repunit 111 in octal (base 8) and the palindrome 1001001 in binary (base 2)*Prime Curios
Fans of the Big Bang Theory on TV know that Leonard refers to 73 as the "Chuck Norris of Numbers" After Sheldon points out that : 73 is the 21st prime, and it's mirror image 37 is the 12th prime. This enigma is the only known such combination.
Sheldon failed to mention that 73 is also the 37th odd number. And it's interesting that this is the only known emirp pair where one is one less than twice the other.
And 73 is the smallest prime factor of a googol + 1 *Prime Curios
73^3 =343= (3+4)^3
If you want to represent all numbers as a sum of sixth powers, at times you will need to use at least six of them.
A good time to introduce you student's to a nice way to find many digits of pi, ( pick a relatively close apppx of pi (I'll use 2.5) and call it x, then x+ sin(x) is a better approximation, and repeating continues to give more and more digits of pi up to limits of calculator For 2.5 we get 3.098 -> 3.14157 -> 3.141592654 . (student's might be challenged for why (and when) this works).
Thomas Jefferson ran against Aaron Burr for president, and they both got 73 votes.
The sum of the first 73 odd primes, is divisible by 73
73 =8^2 + 8^1 + 8^0
The smallest prime that divides a 7-digit number of the form p0p,
73 is the smallest prime factor of A Googol +1
The 73rd triangular number is equal to 73 times the reversal of 73, *Prime Curios
73*37=2701 = the sum of the integers from 1 to 73
A winning solution to the 15-hole triangular peg solitaire game using this method is: (4,1), (6,4), (15,6), (3,10), (13,6), (11,13), (14,12), (12,5), (10,3), (7,2), (1,4), (4,6), (6,1).
Not only does this solution leave the final peg in the original empty hole, but the sum of all the x,y hole numbers in the solution is prime (179) By the way, if you only sum the values of the landing holes, that's prime also (73).
There are exactly 73 primes, beginning with the prime 1093 and ending with the prime 1613, where 10932 + 10972 + ... + 16132 = 117072. This is the first instance of a prime number of primes comprising the left member of such an equation.
The smallest prime that is the middle term of three consecutive numbers each expressible as a sum of two nonzero squares: 72 = 62 + 62 ; 73 = 32 + 82 ; 74 = 52 + 72. *Prime Curios
And of course, for Pi Day, we need the world's most accurate Pi Chart
The 74th Day of the Year
74 is related to an open question in mathematics since 742 + 1 is prime. Hardy and Littlewood conjectured that asymptotic number of elements in this sequence, primes = n2 + 1, not exceeding n is approximately \(c \frac {\sqrt{n}} {log(n)}\) for some constant c. There was a $1000 prize for best solution to an open sequence during 2015 and submitting it to OEIS, details here
74 is the sum of the squares of two consecutive prime numbers. 5^2 + 7^2 Euler pointed out that any number that is twice a number that is the sum of two squares, will also be the sum of two squares.
A hungry number is number in the form 2n that eats as much pi as possible, for example 25 is the smallest power of two that contains a 3. The smallest power that contains the first three digits of pi, 314 is 274 (eating e seems much harder for powers of 2). Students might explore hungry numbers with other bases
22796996699 is the 999799787th prime. Note that the sum of digits of the nth prime equals the sum of digits of n, and both sum to 74. The number 74 is the largest known digit sum with this property (as of August 2004). *Prime Curios
There are 74 different non-Hamiltonian polyhedra with a minimum number of vertices. A Hamiltonian Polyhedra, like the Dodecahedron, is a polyhedron that has a connected circuit along the 20 vertices using distinct edges. Hamilton created a game he called the Icosian game whose object was to find the path. He used pegboard holes on the planer graph of the dodecagon. Every Platonic solid, and many others polyhedra, have a Hamiltonian cycle
The 75th Day of the Year:
the aliquot divisors of 75 are 1,3,5,15, and 25. Their sum is a perfect square, 49. Their product is also a perfect square, 5625. (Can you find other numbers with this property?)
75 is also the larger of the smallest pair of betrothed (quasi-amicable) numbers. 48 and 75 are a betrothed pair since the sum of the proper divisors of 48 is 76 and 75+1 = 76 and the sum of the proper divisors of 75 is 49, with 48+1=49. (There is only a single other pair of betrothed numbers that can be a year day)
75 and 76 form the first pair of adjacent numbers in base ten which are NOT a palindrome in any base \( 2 \leq b \leq 10 \)
275 + 75 is prime
75 is a Keith # or repfigit (75 appears in a Fibonacci-like sequence created by its digits) 7, 5, 12, 17, 29, 46, 75 ... (75 is the sixth of seven year days which are repfigits. Can you find the others?)
If you count all the ways 4 competitors can rank in a competition, allowing for the possibility of ties, there are 75 such possible rankings.
These are called Fubini Numbers, named for Italian mathematician Guido Fubini.
Hare (2005) has shown that any odd perfect number must have 75 or more prime factors.(Nelson (2006)showed that at least nine of them must be distinct.)
The 76th Day of the Year:
76 is an automorphic number because the square of 76 ends in 76. (5 and 6 are automorphic because 52 ends in five and 62 ends in six). There is one other two digit automorphic number (it should be easy to find) but can you find the three digit ones?
In general there are two that can be found for n digit numbers, but sometimes one of them doesn't have n digits, but n-1. One of the squares (that has n digits) is the square root of 5^(2^n) where n is the number of digits, divided by 10^n. so for three digits 5^8 is the square of one of the numbers, (625) and the other is 10^3 + 1 - this first result, or 1001 - 625 = 376. Alas both solutions are too big to be year dates. John Cook has some information with feedback from followers that explains more. The relation between automorphic number and powers of ten is interesting. An n digit automorphic number A times (A-1) will always be a multiple of 10^n. 76 x 75 for example, is 5700. 376 x 375 = 141000.
If you omit numbers that terminate in zero, the only multidigit numbers that have a square that ends in the original number must end in 25 or 76. \( 76^2 = 5776\), \( 376^2 = 141376\) , \(9376^2 = 87909736\)
76= 8 + 13 + 21 + 34 the sum of four consecutive Fibonacci numbers
76 is the number of 6 X 6 symmetric permutation matrices.
Seventy Six is an unincorporated community in Clinton County, Kentucky, United States. Seventy Six is 6.9 miles north of Albany( and 46 miles west of 88, ky.). Its post office has been closed.
76 can be partitioned into distinct prime integers in 76 ways. There are no other such numbers. *Prime Curios. (3 + 73 for example, is one such partit
The 78th Day of the Year
78 is the smallest number that can be written as the sum of 4 distinct squares in 3 ways. *What's Special About This Number
78 is the sum of the first twelve integers, and thus a triangular number.
The cube of 78 is equal to the sum of three distinct cubes, 783 = 393 + 523 + 653
(Historically, it seems Ramanujan was inspired by a much smaller such triplet 63 = 33 + 43 + 53
77 and 78 form the fourth Ruth-Aaron pair, named for the number of home runs hit by Babe Ruth, 714, and the number when Aaron broke the record, 715 (he hit more afterward). They are consecutive numbers that have the same sums of their prime factors (77 = 7*11, 78 = 2*3*13, and 7+11 = 2+3+13).
78, is a sphenic number, having 3 distinct prime factors. (A good word for students to learn) 78=2*3*13
78 is the 12th Triangular number, the sum of the digits from 1 to 12.
78 is a palindromic number in bases 5 (3035, and base 7 (141>7 (77 which is a palindrome itself, is not a palindrome in any smaller base.
78 is the number of cards in a tarot deck containing the 21 trump cardsand the 56 suit cards. *Wik
Ron Graham proved that every number greater than or equal to 77 , can be partitioned into a sum of positive integers so that the sum of their reciprocals is one. 78 = 2 + 6 + 8 + 10 + 12 + 40, and 1/2 + 1/6 + 1/8 + 1/10 + 1/12 + 1/40 = 1
The 79th Day of the Year:
79 is the smallest prime whose sum of digits is a fourth power. *Prime Curios (the second smallest is its reversal, 97)
78*79 = 6162 (note that the product of consecutive numbers produces a number that is the concatenation of two successive numbers 61 and 62 in ascending order (and 61 is prime). (Can you find another number, not necessarily prime, so that n(n-1)= a concatenation of consecutive numbers?)
79 = 27 - 72
79 is the smallest number that can not be represented with less than 19 fourth-powers. (Before you read blythly on, there are three more year days that also require the sum of 19 fourth-powers... find one.)
Each of the numbers 1 to 79 gives a larger number when you write out its English name and add the letters using a=1, b=2, c=3, ... (but 80 gives 74)*Prime Curios
79 = 11 + 31 + 37. Curiously, the sum holds for the reversals: 97 = 11 + 13 + 73, and all are primes.
On page 79 of the novel Contact by Carl Sagan, it says that no astrophysical process is likely to generate prime numbers.*Prime Curios
279 is the smallest power of 2 which is greater than Avogadro's number
79 is the largest number as the sum of the product of two successive primes.
1079 has been called the "Universe number" because it is considered a reasonable lower limit estimate for the number of atoms in the observable universe. *Prime Curios
79 is an Emirp, a prime whose digit reversal is another prime. and which is the sum of three other Emirps, and also true for the sum of their reversals 79 = 11 + 31 + 37and 97 = 11 + 13 + 73.
279 = 604462909807314587353088 is the smallest pandigital number of the form 2 to the power of prime.*Prime Curios
There are 79 ways to place four non-attacking chess kings on a 4 × 4 board.
79 square cm is the typical surface area of an average brick. *Jennifer Li
The 80th Day of the Year:
There are 80 four-digit primes which are concatenations of two-digit primes. (3137 is one example, can you find the rest?) *Prime Curios!
80 in Roman Numerals is not suitable for minors, LXXX,
The Pareto principle (sometimes called the 80-20 rule) says that, for many events, roughly 80% of the effects come from 20% of the causes, ie, \( \approx 80\% \) of the accidents are caused by 20% of the drivers.
\(n*2^{n-1} \) gives the number of edges (segments) in a n-dimensional cube, and in the 5th dimension, (went there once in a dream) there are 80 edges, 5*24
(It also has eighty two-dimensional square faces.)
And 80 is the smallest number diminished by taking its sum of letters (writing out its English name and adding the letters using a=1, b=2, c=3, ...) *Tanya Khovanova
In 1719 Paul Halcke showed that the product of the aliquot divisors of 80 equals the fourth power of 80. The only year numbers for which this is true is 48 and 80.
80 and 86 combine to form the largest four digit vampire number, 6880. Note 80 x 86 = 6880 and the same four digits are used in both sides of the equality.
The 82nd Day of the Year:
82 is the sum of the 10th(8+2) prime and the 16th(8x2) prime. It is the smallest number with this property. Can you find the next?
82 is a happy number. Take the sum of the square of the digits, repeat on the result, and you eventually arrive at 1.
82 is the number of different ways you can arrange 6 regular hexagons by joining their adjacent sides:
82 can be written as : The sum of Fibonacci numbers, 82 = 1 + 5 + 21 + 55 The sum of consecutive integers, 82= 19 + 20 + 21 + 22 and as the sum of squares 82= 12 + 92 *What's Special About This Number
86 in base 6 is a repdigit, and thus a palindrome (222) that makes it equal to twice the digits of the beast number raised to consecutive power, 86 = 2* (6^0 + 6^1 + 6^2)
Kentucky Highway 86 is only a fraction of a mile greater than 86/2. It runs from Union Star to US 62 near Cecillia.
The 87th Day of the Year:
87 is the sum of the squares of the first four primes is 87. \(87 = 2^2 + 3^2 + 5^2 + 7^2 \)
87 = 3 * 29, \(87^2 + 3^2 + 29^2 and 87^2 - 3^2 - 29^2 \)are both primes
Among Australian cricket players, it seems, 87 is an unlucky score and is referred to as "the devil's number", supposedly because it is 13 runs short of 100.
87 is the third consecutive day that is semiprime (the product of two primes), 85, with 86 and 87 are the second smallest three consecutive numbers such all three are products of two primes. *Don S McDonald
And 87 is, of course, the number of years between the signing of the U.S. Declaration of Independence and the Battle of Gettysburg, immortalized in Abraham Lincoln's Gettysburg Address with the phrase "fourscore and seven years ago..."
87 is the largest number that yields a prime when any of the one-digit primes 2, 5 or 7 is inserted between any two digits. The only other such number is 27 (and trivially, the 1 digit numbers). *Prime Curios
5! - 4! - 3! - 2! - 1! = 87. Remember the old puzzle of making numbers with four 4's. What numbers could you make with the first five factorials using only the four basic arithmetic functions between them
The 88th Day of the year:
882 = 7744, it is one of only 5 numbers known whose square has no isolated digits. (Can you find the others?) [Thanks to Danny Whittaker @nemoyatpeace for a correction on this.] I find it beautiful that a
The 89th Day of the year:
89 is the fifth Fibonacci prime and the reciprocal of 89 starts out 0.011235... (generating the first five Fibonacci numbers) *Prime Curios It actually generates many more, but the remainder are hidden by the carrying of digits from the two digit Fibonacci numbers. (The next digit, for instance is a 9 instead of an eight because it includes the tens digit of the next Fibonacci number, 13.)
89 is the 11th Fibonacci number, and it is not divisible by any smaller Fibonacci numbers. \( F_m divides F_n \) only if m divides n. Since 89 is the 11th Fibonacci number so it is not divisible by any smaller Fibonacci number. This can help if finding possible factors for numbers are knowing if they are prime. 377 is the 14th Fibonacci number, and 14 is divisible by 7, so 377 is not prime, and is divisible by by F<sub>_7</sub> which is 13. 377 = 13 x 29.
One more note about Fibonacci numbers that ties them to a sequence of hypotenii of right triangles, if you look at Fibonacci numbers beginning with 5; 5, 8, 13, 21, 34, 55, 89... Every other one is the hypotenuse of a Pythagorean triangle. For this case, 39, 80, 89 are the three sides. But if you look at the previous one, 16, 30, 34 you might notice that the sum of these sides is 89, and such is true for each of them.
89 is a factor of 2^11 - 1, the smallest factorable Mersenne Number with a prime exponent.
89 is the 24th prime number,
The base of the Statue of Liberty is 89 feet tall.
89 is an invertible number (rotation by 180 degrees produces a different number, 68) Others refer to such rotations that produce another number as Strobogrammatic. Even another term for them is numeric ambigrams. Which ever term you use, it is the sum of 1+8+11+69, four strobogrammatic numbers.
and 89 can be expressed by the first 5 integers raised to the first 5 Fibonacci numbers: 11 + 25 + 33 + 41+ 52
If you write any integer and sum the square of the digits, and repeat, eventually you get either 1, or 89 (ex: 16; \( 1^2 + 6^2 = 37; 3^2 + 7^2 = 58; 5^2 + 8^2 = 89 \) Numbers that iterate to 1 are called Happy numbers. numbers that do not iterate to 1 eventually fall into the repeating cycle with the eight values 4, 16, 37, 58, 89, 145, 42, and 20.
91^2 - 89 ^2 = 360. *Gary Croft pointed out in a post that if you take the 24 numbers up to 89 that are not divisible by any of 2, 3, or 5 (he uses this set for a very efficient prime sieve) they pair up so that the difference of their squares are multiples of 360 (89^2 - 1^2 = 360 x 22; 83^2 - 7^2 = 360 x 19; ....)
89 = 81 + 92 There are two three digit year dates that share this property, abc = a^1 + b^2 + c^3
An Armstrong (or Pluperfect digital invariant) number is a number that is the sum of its own digits each raised to the power of the number of digits. For example, 371 is an Armstrong number since \(3^3+7^3+1^3 = 371\). There are exactly 89 such numbers, including two with 39 digits. (115,132,219,018,763,992,565,095,597,973,522,401 is the largest) (Armstrong numbers are named for Michael F. Armstrong who named them for himself as part of an assignment to his class in Fortran Programming at the University of Rochester \)
89 is the smallest prime (indeed the smallest positive integer) whose square (7921) and cube (704969) are likewise prime upon reversal. *Prime Curios
And from our strange measures category, A Wiffle, also referred to as a WAM for Wiffle (ball) Assisted Measurement, is equal to a sphere 89 millimeters (3.5 inches) in diameter – the size of a Wiffle ball, a perforated, light-weight plastic ball frequently used by marine biologists as a size reference in photos to measure corals and other objects. The spherical shape makes it omnidirectional and perfect for taking a speedy measurement, and the open design also allows it to avoid being crushed by water pressure. Wiffle balls are a much cheaper alternative to using two reference lasers, which often pass straight through gaps in thin corals. A scientist on the research vessel EV Nautilus is credited with pioneering the technique *Wik
The sum of all the prime numbers up to and including 89 is 963. If you eliminate the single even prime, 2, the total is 961 = 31^2. This is the smallest such sum of primes for which this is true.
The concatenation of all odd primes starting from 89 and counting in reverse is prime.*Prime Curios (so what if it starts with 83?
89 is a Pythagorean Prime, one that is the sum of two squares. 8^2 + 6^2
22 + 33 + 55 + 77 + 1111 + ... + 8989 is prime.
Hellin's law states that twins occur once in 89 births, triplets once in 892 births, and quadruplets once in 893 births, and so forth. This approximation came before the advent of fertility methods. *Prime Curios
89892 = 80802121. 89 is the smallest prime, P so that PP2 is of the form XXYY, *Prime Curios
89^2 - 2 = 7919, the 1000th prime, so there are exactly 1000 primes between 1 and 892
89 is a palindrome in base 8 (131)
How about some sums of sequential primes raised to their own power....that are prime!!!
From the clever Tweets of Srinivasa Raghava K \( 2^2 + 3^3 = 13 \) and
\(2^2 + 3^3 + 5^5 + 7^7 = 826699\) also prime, and
\(2^2 + 3^3 + \dots + 89^{89} \) is BIG... and Prime
Oklahoma City, Ok. was founded in the Land Run of 89, when property in the Indian Nation was opened to white settlers.
Double 89 and add 1, you get a prime. Keep doing it and you'll get a sequence of six such primes. Primes p for which 2p + 1 are also prime are called Sophie Germain primes, after a great female mathematician.
US 89 is called the National Parks Hwy, and runs, almost literally, through Yellowstone Natl Park, and Links it to six more.
The 90th day of the year;
90 is the only number that is the sum of its digits plus the sum of the squares of its digits. (Is there any interesting distinction to the rest of the numbers for which this sum is more (or less) than the original number?)
\( \frac{90^3 - 1}{90 - 1} \) is a Mersenne prime.
90 = 3^2 + 9^2 = 3^2 + 3^4
90 is a Harshad (Joy Giver) number since 90 is divisible by the sum of its digits
90 is the smallest number having 6 representations as a sum of four positive squares
90 is the number of degrees in a right angle. Moreover, as a compass direction, 90 degrees corresponds to east. Which reminds me of a fun math joke:"The number you have dialed is imaginary. Please rotate you phone by 90 degrees and dial again."
And 90 is the sum of the first 9 consecutive even numbers, the sum of consecutive integers in two different ways, the sum of two consecutive primes, and of six consecutive primes(in two distinct ways), and the sum of five consecutive squares. (all proofs left to the reader.)
(903 - 1)/(90 - 1) is a Mersenne prime. *Prime Curios The bases in Major League Baseball are 90 feet apart.
Sixty Six is an unincorporated community in Orangeburg County, South Carolina, United States. Sixty Six is located along U.S. Route 21, north of Branchville.
66 is a semi-perfect number, since some subset of it's proper divisors add up to 66.(11+22+33=66 there is another way to do it also )
And just to conjure up one more variant on the number of the beast, 666, there are exactly 66 six-digit primes with distinct non-prime digits.
And just to conjure up one more variant on the number of the beast, 666, there are exactly 66 six-digit primes with distinct non-prime digits.
The 67th Day of the Year:
67 is the largest prime which is not the sum of distinct squares.
Mersenne thought 2^67 - 1 was prime.; In 1867 Lucas proved that it was not prime, but could not find the factors. It was not until October 31, 1903 that Frank Nelson Cole found the factors. ;During Cole's so-called "lecture", he approached the chalkboard and in complete silence proceeded to calculate the value of M67 with the result being 147,573,952,589,676,412,927. Cole then moved to the other side of the board and wrote 193,707,721 × 761,838,257,287, and worked through the tedious calculations by hand. Upon completing the multiplication and demonstrating that the result equaled M67 Cole returned to his seat, not having uttered a word during the hour-long presentation. His audience greeted the presentation with a standing ovation. Cole later admitted that finding the factors had taken "three years of Sundays." *Wik
It is the 19th prime number and the sum of five consecutive primes ending in 19 (7 + 11 + 13 + 17 + 19)
The maximum number of internal pieces possible if a circle is cut with eleven lines. These are sometimes called "lazy caterer's numbers." \( 67 = \binom{11}{0} + \binom {11} {1} + \binom {11}{2} \)
67 is also the smallest prime which contains all ten digits when raised to the tenth power. *Prime Curios
67^10 =1822837804551761449
67 in Roman Numerals if LXVII. If you evaluate that using the a=1, b=2 method, the sum LXVII = 76, the reversal of the digits of 67.
67 is the largest known prime for which 2^p does not contain any zeros.
and Jim Wilder @wilderlab sent 67 = 26 + 21+ 20 = 26 + 21 + 20 = 67
and @expert_says added several more. Students might be shown one relationship, and encouraged to discover others:
67=1² + 1² + 1⁷ + 2⁶ =12+12+17+26
67=1² + 1³ + 1⁶ + 2⁶ =12+13+16+26
67=1² + 1⁴ + 1⁵ + 2⁶= 12+14+15+26
67=1³ + 1³ + 1⁵ + 2⁶=13+13+15+26
67=1³ + 1⁴ + 1⁴ + 2⁶=13+14+14+26
And one smoot is equal to 67 inches.
67 is palindromic in the consecutive bases 5 (2325) and 6 (1516).
The 68th Day of the Year:
if you searched through pi for all the two digit numbers, the last one you would find is 68. The string 68 begins at position 605 counting from the first digit after the decimal point. (What is the last single digit numeral to appear? One might wonder how far out the string would you have to go to find all possible three digit numbers? )
68 is the largest known number to be the sum of two primes in exactly two different ways:
68=7+61=31+37. All higher even numbers that have been checked are the sum of three or more pairs of primes
68 is a stobogrammatic number, rotated it is 89. Some consider only invertible numbers (rotated they form the same value, like 181) as strobograms. HT to Paul O'Malley By the way, it's the smallest composite number with a prime strobogrammatic partner.
There are exactly 68 ten digit binary numbers in which each digit is the same as one of it's adjacent digits.
68 is the smallest composite number that can be read as a prime number when it is rotated 180o HT Jim Wilder @wilderlab.
And a historical oddity, in 46 BCE, as a result of Julius Caesar's Calendar adjustment, there were 68 days inserted between November and December.
68 is also a Happy number since 68 → 6^2 + 8^2 = 100 → 1^2 + 0^2 + 0^2 = 1
\( 2^68\) is the smallest power of two that is pandigital, with all ten decimal digits. It is a number 21 digits long. *@Fermat's Library
The 69th Day of the Year:
the square and the cube of 69 together contain all ten numerals. 692 = 4761, 693 =328509
1069+69 is prime and; 10069-69 is prime
On Many scientific calculators, 69! is the largest factorial that can be calculated, with an overflow error for larger numbers. 69! is appx 1.711 (1098)
Don S. McDonald @McDONewt pointed out that \( \binom{69}{5}\) = 11238513, 7 Fibonacci #'s almost in order.
69 is a strobogrammatic pair with itself. It is the smallest such number with distinct numbers. Reversing the order of its digits gives 96, another strobogrammatic self-pair. And for a bonus, the sum of the divisors of 69 is 96.
The first squared square to be found was a square filled with 69 different smaller squares. ( electrical network theory was used to make the discovery, previously most mathematicians felt that were not likely to be any squared squares see Jan 21).. The first squared square was published in 1938 by Roland Sprague who found a solution using several copies of various squared rectangles and produced a squared square with 55 squares, and side lengths of 4205
No squared square can be made with less than 21 squares(shown below)
 |
| Lowest-order perfect squared square *Wik |
\$ 3869 = 62^2 + 05^2 \$<BR>\$ 6205 = 38^2 + 69^2 \$
I quickly seized the moment to coin the term for these as Amicable Sums of Squares (just don't abbreviate it.)
The 70th Day of the Year:
70 is the smallest "Weird" number. In number theory, a weird number is a natural number that is abundant but not semiperfect. In other words, the sum of the proper divisors (divisors including 1 but not itself) of the number is greater than the number, but no subset of those divisors sums to the number itself.
The 70th Day of the Year:
70 is the smallest "Weird" number. In number theory, a weird number is a natural number that is abundant but not semiperfect. In other words, the sum of the proper divisors (divisors including 1 but not itself) of the number is greater than the number, but no subset of those divisors sums to the number itself.
All the primes in the 70's, are emirps, primes that are still prime when you reverse the order of the digits, 71----17 etc.
270 = 1180591620717411303424. The sum of the digits is 70, and if you reverse the order, 424303114717026195081, it is a prime #.
\( 1^2 + 2^2 + 3^2 + \cdots + 24^2 = 70^2 \) Such numbers (sums of first n squares) are called Square Pyramidal Numbers (This one actually has a relationship to the Leech Lattice and String Theory)
Several languages, especially ones with vigesimal number systems, do not have a specific word for 70: for example, French soixante-dix "sixty-ten"; Danish halvfjerds, short for halvfjerdsindstyve "three and a half score". (For French, this is true only in France; other French-speaking regions such as Belgium, Switzerland, Aosta Valley and Jersey use septante.) *Wik
270 = 1180591620717411303424. The sum of the digits is 70, and if you reverse the order, 424303114717026195081, it is a prime #.
\( 1^2 + 2^2 + 3^2 + \cdots + 24^2 = 70^2 \) Such numbers (sums of first n squares) are called Square Pyramidal Numbers (This one actually has a relationship to the Leech Lattice and String Theory)
Several languages, especially ones with vigesimal number systems, do not have a specific word for 70: for example, French soixante-dix "sixty-ten"; Danish halvfjerds, short for halvfjerdsindstyve "three and a half score". (For French, this is true only in France; other French-speaking regions such as Belgium, Switzerland, Aosta Valley and Jersey use septante.) *Wik
70 is the second smallest number where the sum of its divisors is a perfect square. \(1 + 2 + 5 + 7 + 10 + 14 + 35 + 70= 12^2 = 144\) There are only three year dates (to my knowledge) for which the sum of the divisors is a square. They all three occur in this MathFacts page, 66, 70, and 81. 66 and 70 even have the same total.
The 71st Day of the Year:
712=5041 = 7! +1! *Prime Curios 4! +1, and 5!+1 are also squares but not the factorial of the digits. Whether there is a larger value of n for which n! + 1 is a perfect square is still an open question, called the Brocard problem after Henri Brocard who asked it in 1876. It has been proven that no other numbers exist less than 109. *Professor Stewart's Incredible Numbers Cliff Pickover, wrote that 71 is the largest known prime, p, such that p2 is the sum of distinct factorials.
A Cute way of writing the above, \(\sqrt{7! + 1} = 71 \)
71 is the first two decimal digits of the expression of e=2.718281828459045...
71 is the largest number that occurs as a prime factor of the order of a sporadic group.*Wik
71 is the first of three consecutive primes that are all still primes when their digits are reversed. (is there another such occurrence?) All the primes in the 70's, are emirps, primes that are still prime when you reverse the order of the digits, 71----17 etc.
and too good to leave out, 71 is the only two-digit number n such that (nn-n!)/n is prime. *Tanya Khovanova, Number Gossip (Be the first on your block to find a three digit example.)
In 1935, Erdős and Szekeres proved that 71 points (no three on a single line) are required to guarantee there are six that form a convex hexagon, although 17 points are thought to be sufficient. (In 1998, the upper bound was reduced to 37.) *Prime Curios
713=357,911 where the digits are the odd numbers 3 to 11 in order * @Mario_Livio
713 is also the only cube of a 2-digit number that ends in 11. There is only one 1digit cubed that ends in 1, and only one three digit cubed that ends in 111(Don't just sit there children, go find them!). Could there be a four digit cube that ends in 1111
The sum of all the prime numbers up to, and including 71 is not prime, but it is divisible by 71. (This works for 5 as well, and for 369119, and that's the only ones we know about.) 71 will also divide the sum of all the primes smaller than 71. It is the smallest such prime to be a proper divisor of the sum of all smaller primes. What's next?
71 is expressible as the sum of successive composite numbers in two ways, 22 + 23 + 24 = 71 = 35 + 36 There are no smaller numbers for which this is true. It is also the sum of three consecutive primes, 19 + 23 + 29
A 71-digit prime is formed by intertwining the even (from 2 to 40) and the odd (from 1 to 39) numbers (214365...374039) *Prime Curios By my calculation the only smaller such prime is the four digit 2143
71 is the largest prime p that humans will ever discover such that 2p doesn't contain the digit 9. *Cliff Pickover (I do wonder how they go about proving such facts.)
The sum of the prime numbers up to 71 is 639=9*71
The smallest prime that remains prime when inserting one, two, three, or four zeros between each digit. *Prime Curios So 701, 7001, 70001, and 700001 are all prime. Students might search for numbers that can include one zero, or two, etc.
The Monster Group is the largest sporadic simple group and contiains appx 8 x 10^53 elements. Grant Sanderson or pointed out that its largest factor is 71. The others form a stange patter with each succesive larger factor having a lower than or equal exponent to the previous (except for one strange counterexample that makes it even more weird. \( 2^{46} x 3^{20} x 5^9 x 7^5 x 11^2 ^ 13^3 x 17 x 19 x 23 x 29 x 31 x 41 x 47 x 59 x 71\)
The 72nd Day of the Year:
72 is a pronic, heteromecic, or oblong number (and sometimes pronic is spelled promic). They are numbers that are the product of two consecutive integers Oblong numbers have the property that if they are used in infinite nested radicals, they produce an integer, \(\sqrt(72+\sqrt(72+\sqrt(72+...))) = 9 \)
72 is the smallest number whose fifth power is the sum of five smaller fifth powers: \(19^5 + 43^5 + 46^5 + 47^5 + 67^5 = 72^5\).
The rule of 72 was once a commonly used approximation in banking and finance for the time it took an investment to double at r%. For a 5% investment, the approximate period would be 72/5 = 14.4 years. The rule applies to compound interest. The rule is based on an approximation of ln(2) = .693..
In a plane, the regular pentagon has exterior angles of 72o
The Rhombicuboctahedron or Great Rhombicuboctahedron is an Archimedian solid that has 72 edges. It has 12 faces that are squares, 8 faces that are hexagons, and six faces that are octagons, for a total of 26 faces in all. Knowing the number of edges and faces, good students can calculate the number of vertices using Euler's Gem. (there is a lesser Rhombicuboctahedron or just Cubicuboctahedron which is a faceted version of the greater)
72 the sum of four consecutive primes (13 + 17 + 19 + 23), as well as the sum of six consecutive primes (5 + 7 + 11 + 13 + 17 + 19). Good plane geometry students know that the exterior angles of a regular pentagon measure 72 degrees each.
72 is 23+ 32. Is is the smallest such number where the numbers are distinct primes.
72 is the smallest number whose fifth power is the sum of five smaller fifth powers: 195 + 435 + 465 + 475 + 675 = 725.*Wik
In typography, point sizes are measured in 1/72 of an inch, 72-point characters are 1 inch tall.
72 is the smallest number that can be expressed as the difference of the squares of consecutive primes in two distinct ways: {192 - 172} and {112 - 72}
The 71st Day of the Year:
712=5041 = 7! +1! *Prime Curios 4! +1, and 5!+1 are also squares but not the factorial of the digits. Whether there is a larger value of n for which n! + 1 is a perfect square is still an open question, called the Brocard problem after Henri Brocard who asked it in 1876. It has been proven that no other numbers exist less than 109. *Professor Stewart's Incredible Numbers Cliff Pickover, wrote that 71 is the largest known prime, p, such that p2 is the sum of distinct factorials.
A Cute way of writing the above, \(\sqrt{7! + 1} = 71 \)
71 is the first two decimal digits of the expression of e=2.718281828459045...
71 is the largest number that occurs as a prime factor of the order of a sporadic group.*Wik
71 is the first of three consecutive primes that are all still primes when their digits are reversed. (is there another such occurrence?) All the primes in the 70's, are emirps, primes that are still prime when you reverse the order of the digits, 71----17 etc.
and too good to leave out, 71 is the only two-digit number n such that (nn-n!)/n is prime. *Tanya Khovanova, Number Gossip (Be the first on your block to find a three digit example.)
In 1935, Erdős and Szekeres proved that 71 points (no three on a single line) are required to guarantee there are six that form a convex hexagon, although 17 points are thought to be sufficient. (In 1998, the upper bound was reduced to 37.) *Prime Curios
713=357,911 where the digits are the odd numbers 3 to 11 in order * @Mario_Livio
713 is also the only cube of a 2-digit number that ends in 11. There is only one 1digit cubed that ends in 1, and only one three digit cubed that ends in 111(Don't just sit there children, go find them!). Could there be a four digit cube that ends in 1111
The sum of all the prime numbers up to, and including 71 is not prime, but it is divisible by 71. (This works for 5 as well, and for 369119, and that's the only ones we know about.) 71 will also divide the sum of all the primes smaller than 71. It is the smallest such prime to be a proper divisor of the sum of all smaller primes. What's next?
71 is expressible as the sum of successive composite numbers in two ways, 22 + 23 + 24 = 71 = 35 + 36 There are no smaller numbers for which this is true. It is also the sum of three consecutive primes, 19 + 23 + 29
A 71-digit prime is formed by intertwining the even (from 2 to 40) and the odd (from 1 to 39) numbers (214365...374039) *Prime Curios By my calculation the only smaller such prime is the four digit 2143
71 is the largest prime p that humans will ever discover such that 2p doesn't contain the digit 9. *Cliff Pickover (I do wonder how they go about proving such facts.)
The sum of the prime numbers up to 71 is 639=9*71
The smallest prime that remains prime when inserting one, two, three, or four zeros between each digit. *Prime Curios So 701, 7001, 70001, and 700001 are all prime. Students might search for numbers that can include one zero, or two, etc.
The Monster Group is the largest sporadic simple group and contiains appx 8 x 10^53 elements. Grant Sanderson or pointed out that its largest factor is 71. The others form a stange patter with each succesive larger factor having a lower than or equal exponent to the previous (except for one strange counterexample that makes it even more weird. \( 2^{46} x 3^{20} x 5^9 x 7^5 x 11^2 ^ 13^3 x 17 x 19 x 23 x 29 x 31 x 41 x 47 x 59 x 71\)
The 72nd Day of the Year:
72 is a pronic, heteromecic, or oblong number (and sometimes pronic is spelled promic). They are numbers that are the product of two consecutive integers Oblong numbers have the property that if they are used in infinite nested radicals, they produce an integer, \(\sqrt(72+\sqrt(72+\sqrt(72+...))) = 9 \)
72 is the smallest number whose fifth power is the sum of five smaller fifth powers: \(19^5 + 43^5 + 46^5 + 47^5 + 67^5 = 72^5\).
The rule of 72 was once a commonly used approximation in banking and finance for the time it took an investment to double at r%. For a 5% investment, the approximate period would be 72/5 = 14.4 years. The rule applies to compound interest. The rule is based on an approximation of ln(2) = .693..
In a plane, the regular pentagon has exterior angles of 72o
72 the sum of four consecutive primes (13 + 17 + 19 + 23), as well as the sum of six consecutive primes (5 + 7 + 11 + 13 + 17 + 19). Good plane geometry students know that the exterior angles of a regular pentagon measure 72 degrees each.
72 is 23+ 32. Is is the smallest such number where the numbers are distinct primes.
72 is the smallest number whose fifth power is the sum of five smaller fifth powers: 195 + 435 + 465 + 475 + 675 = 725.*Wik
In typography, point sizes are measured in 1/72 of an inch, 72-point characters are 1 inch tall.
72 is the smallest number that can be expressed as the difference of the squares of consecutive primes in two distinct ways: {192 - 172} and {112 - 72}
The number of integers less than 72 and relatively prime to it is 24. The same is true for the numbers 78, 84, and 90. This is the smallest set of four numbers in arithmetic sequence with the same value of Euler's phi function or totient function. The next string of four begins at 216. It also has an arithmetic difference of 6, and the repeated totient is (wait for it....) 72
The 73rd Day of the Year
On non-leap years, the 73rd year day is Pi Day, March 14. 73 first occurs in the 299th digit of Pi, well behind its prime pair partner 71, which appears in the 39th position.
73 is the alphanumeric value of the word NUMBER: 14 + 21 + 13 + 2 + 5 + 18 = 73 a prime number*Tanya Khovanova, Number Gossip;
Expressing 73 as four 4's using the original rules of using only the four basic arithmetic functions with parentheses and concatenation has not been solved. It is one of the most difficult primes under any of the rule sets I know. (You can find a short history of the Four 4's problem here
 |
| Today, have your Pi(e) both ways! |
On non-leap years, the 73rd year day is Pi Day, March 14. 73 first occurs in the 299th digit of Pi, well behind its prime pair partner 71, which appears in the 39th position.
73 is the alphanumeric value of the word NUMBER: 14 + 21 + 13 + 2 + 5 + 18 = 73 a prime number*Tanya Khovanova, Number Gossip;
Expressing 73 as four 4's using the original rules of using only the four basic arithmetic functions with parentheses and concatenation has not been solved. It is one of the most difficult primes under any of the rule sets I know. (You can find a short history of the Four 4's problem here
And if you are stumped, here is one way from Keith Raskin on LInkedIn:
"In the book Mathematical Bafflers, all integers from 0 to 100 are represented by 4 4’s, but square roots, exponentiation, factorials, decimals and infinite repetition (repetends of 4) are allowed.
73 is expressed as [4!(sqrt(4) + sqrt(.4 repeating)] / sqrt(.4 repeating) = [48 + 2/3] / (2/3) = [146/3] x 3/2 = 73"
73 is expressed as [4!(sqrt(4) + sqrt(.4 repeating)] / sqrt(.4 repeating) = [48 + 2/3] / (2/3) = [146/3] x 3/2 = 73"
73 is the largest prime day of the year so that you can append another digit and make another prime six times, 73, 739, 7393, 73939, 739391, 7393913, and 73939133.
73 is the smallest prime that can be expressed as the sum of three cubes, 1^3 + 2^3 + 4^3 =73
The prime number 73 is the repunit 111 in octal (base 8) and the palindrome 1001001 in binary (base 2)*Prime Curios
Fans of the Big Bang Theory on TV know that Leonard refers to 73 as the "Chuck Norris of Numbers" After Sheldon points out that : 73 is the 21st prime, and it's mirror image 37 is the 12th prime. This enigma is the only known such combination.
Sheldon failed to mention that 73 is also the 37th odd number. And it's interesting that this is the only known emirp pair where one is one less than twice the other.
And 73 is the smallest prime factor of a googol + 1 *Prime Curios
73^3 =343= (3+4)^3
If you want to represent all numbers as a sum of sixth powers, at times you will need to use at least six of them.
A good time to introduce you student's to a nice way to find many digits of pi, ( pick a relatively close apppx of pi (I'll use 2.5) and call it x, then x+ sin(x) is a better approximation, and repeating continues to give more and more digits of pi up to limits of calculator For 2.5 we get 3.098 -> 3.14157 -> 3.141592654 . (student's might be challenged for why (and when) this works).
Thomas Jefferson ran against Aaron Burr for president, and they both got 73 votes.
The sum of the first 73 odd primes, is divisible by 73
73 =8^2 + 8^1 + 8^0
The smallest prime that divides a 7-digit number of the form p0p,
73 is the smallest prime factor of A Googol +1
The 73rd triangular number is equal to 73 times the reversal of 73, *Prime Curios
73*37=2701 = the sum of the integers from 1 to 73
Not only does this solution leave the final peg in the original empty hole, but the sum of all the x,y hole numbers in the solution is prime (179) By the way, if you only sum the values of the landing holes, that's prime also (73).
There are exactly 73 primes, beginning with the prime 1093 and ending with the prime 1613, where 10932 + 10972 + ... + 16132 = 117072. This is the first instance of a prime number of primes comprising the left member of such an equation.
The smallest prime that is the middle term of three consecutive numbers each expressible as a sum of two nonzero squares: 72 = 62 + 62 ; 73 = 32 + 82 ; 74 = 52 + 72. *Prime Curios
And of course, for Pi Day, we need the world's most accurate Pi Chart
The 74th Day of the Year
74 is related to an open question in mathematics since 742 + 1 is prime. Hardy and Littlewood conjectured that asymptotic number of elements in this sequence, primes = n2 + 1, not exceeding n is approximately \(c \frac {\sqrt{n}} {log(n)}\) for some constant c. There was a $1000 prize for best solution to an open sequence during 2015 and submitting it to OEIS, details here
74 is the sum of the squares of two consecutive prime numbers. 5^2 + 7^2 Euler pointed out that any number that is twice a number that is the sum of two squares, will also be the sum of two squares.
A hungry number is number in the form 2n that eats as much pi as possible, for example 25 is the smallest power of two that contains a 3. The smallest power that contains the first three digits of pi, 314 is 274 (eating e seems much harder for powers of 2). Students might explore hungry numbers with other bases
22796996699 is the 999799787th prime. Note that the sum of digits of the nth prime equals the sum of digits of n, and both sum to 74. The number 74 is the largest known digit sum with this property (as of August 2004). *Prime Curios
There are 74 different non-Hamiltonian polyhedra with a minimum number of vertices. A Hamiltonian Polyhedra, like the Dodecahedron, is a polyhedron that has a connected circuit along the 20 vertices using distinct edges. Hamilton created a game he called the Icosian game whose object was to find the path. He used pegboard holes on the planer graph of the dodecagon. Every Platonic solid, and many others polyhedra, have a Hamiltonian cycle
 |
| *Wik |
The 75th Day of the Year:
the aliquot divisors of 75 are 1,3,5,15, and 25. Their sum is a perfect square, 49. Their product is also a perfect square, 5625. (Can you find other numbers with this property?)
75 is also the larger of the smallest pair of betrothed (quasi-amicable) numbers. 48 and 75 are a betrothed pair since the sum of the proper divisors of 48 is 76 and 75+1 = 76 and the sum of the proper divisors of 75 is 49, with 48+1=49. (There is only a single other pair of betrothed numbers that can be a year day)
75 and 76 form the first pair of adjacent numbers in base ten which are NOT a palindrome in any base \( 2 \leq b \leq 10 \)
275 + 75 is prime
75 is a Keith # or repfigit (75 appears in a Fibonacci-like sequence created by its digits) 7, 5, 12, 17, 29, 46, 75 ... (75 is the sixth of seven year days which are repfigits. Can you find the others?)
If you count all the ways 4 competitors can rank in a competition, allowing for the possibility of ties, there are 75 such possible rankings.
These are called Fubini Numbers, named for Italian mathematician Guido Fubini.
Hare (2005) has shown that any odd perfect number must have 75 or more prime factors.(Nelson (2006)showed that at least nine of them must be distinct.)
The 76th Day of the Year:
76 is an automorphic number because the square of 76 ends in 76. (5 and 6 are automorphic because 52 ends in five and 62 ends in six). There is one other two digit automorphic number (it should be easy to find) but can you find the three digit ones?
In general there are two that can be found for n digit numbers, but sometimes one of them doesn't have n digits, but n-1. One of the squares (that has n digits) is the square root of 5^(2^n) where n is the number of digits, divided by 10^n. so for three digits 5^8 is the square of one of the numbers, (625) and the other is 10^3 + 1 - this first result, or 1001 - 625 = 376. Alas both solutions are too big to be year dates. John Cook has some information with feedback from followers that explains more. The relation between automorphic number and powers of ten is interesting. An n digit automorphic number A times (A-1) will always be a multiple of 10^n. 76 x 75 for example, is 5700. 376 x 375 = 141000.
If you omit numbers that terminate in zero, the only multidigit numbers that have a square that ends in the original number must end in 25 or 76. \( 76^2 = 5776\), \( 376^2 = 141376\) , \(9376^2 = 87909736\)
76= 8 + 13 + 21 + 34 the sum of four consecutive Fibonacci numbers
76 is the number of 6 X 6 symmetric permutation matrices.
Seventy Six is an unincorporated community in Clinton County, Kentucky, United States. Seventy Six is 6.9 miles north of Albany( and 46 miles west of 88, ky.). Its post office has been closed.
76 can be partitioned into distinct prime integers in 76 ways. There are no other such numbers. *Prime Curios. (3 + 73 for example, is one such partit
and, of course, 76 Trombones Led the Big Parade
The 77th Day of the Year
77 is the only number less than 100 with a multiplicative persistence of 4. Can you find the next? (Multiply all the digits of a number n, repeating with the product until a single digit is obtained. The number of steps required is known as the multiplicative persistence, and the final digit obtained is called the multiplicative digital root of n.) There is not another year day that will have a multiplicative persistence greater than four. [7x7=49, 4x9=36, 3x6=18, 1x8=8]
772 is the smallest square number that can be the sum of consecutive squares greater than 1, \(sum_{k=18}^{28}k^2 = 77^2\) 77^2 = 5929, the concatenation of two primes.
The concatenation of all palindromes from one up to 77 is prime.
77 is equal to the sum of three consecutive squares, \(4^2 + 5^2 + 6^2= 77\) and also the sum of the first 8 primes. *Prime Curios
77 is the sum of the first eight primes, and the sum of three consecutive squares.
77 is the the number of digits of the 12th perfect number. It was discovered in 1876 by Eduoard Lucas. The largest day year that is the number of digits of a prefect number only occurs on a leap year, It is the 14th perfect number. It was discovered in 1951 by Raphael M. Robinson (1911-1995), who also discovered four others in the same year. He is perhaps more famous as the husband of Julia Robinson.
77! + 1 is prime. 77 is the 9th year day for with this attribute, but it is the first composite number for which this is true.
77 is the largest number that cannot be written as the sum of distinct numbers whose sum adds to one.
Ron Graham proved that every number greater than or equal to 77 , can be partitioned into a sum of positive integers so that the sum of their reciprocals is one. It was Graham's doctoral thesis, which he called The 77 Theorem.
The 77th Day of the Year
77 is the only number less than 100 with a multiplicative persistence of 4. Can you find the next? (Multiply all the digits of a number n, repeating with the product until a single digit is obtained. The number of steps required is known as the multiplicative persistence, and the final digit obtained is called the multiplicative digital root of n.) There is not another year day that will have a multiplicative persistence greater than four. [7x7=49, 4x9=36, 3x6=18, 1x8=8]
772 is the smallest square number that can be the sum of consecutive squares greater than 1, \(sum_{k=18}^{28}k^2 = 77^2\) 77^2 = 5929, the concatenation of two primes.
The concatenation of all palindromes from one up to 77 is prime.
77 is equal to the sum of three consecutive squares, \(4^2 + 5^2 + 6^2= 77\) and also the sum of the first 8 primes. *Prime Curios
77 is the sum of the first eight primes, and the sum of three consecutive squares.
77 is the the number of digits of the 12th perfect number. It was discovered in 1876 by Eduoard Lucas. The largest day year that is the number of digits of a prefect number only occurs on a leap year, It is the 14th perfect number. It was discovered in 1951 by Raphael M. Robinson (1911-1995), who also discovered four others in the same year. He is perhaps more famous as the husband of Julia Robinson.
Shortly after John D. Cook published an article on Stewart's Cube, (see Day 83) he got a response from Austin Buchanan who lowered the vertex sums to 77.
" I wondered if Stewart’s cube achieved its structure in the cheapest way. I considered two objectives: (1) minimize the sum of the edges incident to a vertex, and (2) minimize the weight of the worst edge. In both cases, the following cube is optimal.
It improves the first objective from 83 to 77, and the second objective from 61 to 53. To solve the problems, I modeled them as integer programs, and used Gurobi as solver. I’m currently running code for higher-dimensional cubes."
77 is the largest number that cannot be written as the sum of distinct numbers whose sum adds to one.
Ron Graham proved that every number greater than or equal to 77 , can be partitioned into a sum of positive integers so that the sum of their reciprocals is one. It was Graham's doctoral thesis, which he called The 77 Theorem.
It is possible for a sudoku puzzle to have as many as 77 givens, yet lack a unique solution.
77 and 78 form the fourth Ruth-Aaron pair, named for the number of home runs hit by Babe Ruth, 714, and the number when Aaron broke the record, 715 (he hit more afterward). They are consecutive numbers that have the same sums of their prime factors (77 = 7*11, 78 = 2*3*13, and 7+11 = 2+3+13).
77 and 78 form the fourth Ruth-Aaron pair, named for the number of home runs hit by Babe Ruth, 714, and the number when Aaron broke the record, 715 (he hit more afterward). They are consecutive numbers that have the same sums of their prime factors (77 = 7*11, 78 = 2*3*13, and 7+11 = 2+3+13).
The 78th Day of the Year
78 is the smallest number that can be written as the sum of 4 distinct squares in 3 ways. *What's Special About This Number
78 is the sum of the first twelve integers, and thus a triangular number.
The cube of 78 is equal to the sum of three distinct cubes, 783 = 393 + 523 + 653
(Historically, it seems Ramanujan was inspired by a much smaller such triplet 63 = 33 + 43 + 53
77 and 78 form the fourth Ruth-Aaron pair, named for the number of home runs hit by Babe Ruth, 714, and the number when Aaron broke the record, 715 (he hit more afterward). They are consecutive numbers that have the same sums of their prime factors (77 = 7*11, 78 = 2*3*13, and 7+11 = 2+3+13).
78, is a sphenic number, having 3 distinct prime factors. (A good word for students to learn) 78=2*3*13
78 is the 12th Triangular number, the sum of the digits from 1 to 12.
78 is a palindromic number in bases 5 (3035, and base 7 (141>7 (77 which is a palindrome itself, is not a palindrome in any smaller base.
78 is the number of cards in a tarot deck containing the 21 trump cardsand the 56 suit cards. *Wik
Ron Graham proved that every number greater than or equal to 77 , can be partitioned into a sum of positive integers so that the sum of their reciprocals is one. 78 = 2 + 6 + 8 + 10 + 12 + 40, and 1/2 + 1/6 + 1/8 + 1/10 + 1/12 + 1/40 = 1
The 79th Day of the Year:
79 is the smallest prime whose sum of digits is a fourth power. *Prime Curios (the second smallest is its reversal, 97)
78*79 = 6162 (note that the product of consecutive numbers produces a number that is the concatenation of two successive numbers 61 and 62 in ascending order (and 61 is prime). (Can you find another number, not necessarily prime, so that n(n-1)= a concatenation of consecutive numbers?)
79 = 27 - 72
79 is the smallest number that can not be represented with less than 19 fourth-powers. (Before you read blythly on, there are three more year days that also require the sum of 19 fourth-powers... find one.)
Each of the numbers 1 to 79 gives a larger number when you write out its English name and add the letters using a=1, b=2, c=3, ... (but 80 gives 74)*Prime Curios
79 = 11 + 31 + 37. Curiously, the sum holds for the reversals: 97 = 11 + 13 + 73, and all are primes.
On page 79 of the novel Contact by Carl Sagan, it says that no astrophysical process is likely to generate prime numbers.*Prime Curios
279 is the smallest power of 2 which is greater than Avogadro's number
79 is the largest number as the sum of the product of two successive primes.
1079 has been called the "Universe number" because it is considered a reasonable lower limit estimate for the number of atoms in the observable universe. *Prime Curios
79 is an Emirp, a prime whose digit reversal is another prime. and which is the sum of three other Emirps, and also true for the sum of their reversals 79 = 11 + 31 + 37and 97 = 11 + 13 + 73.
279 = 604462909807314587353088 is the smallest pandigital number of the form 2 to the power of prime.*Prime Curios
There are 79 ways to place four non-attacking chess kings on a 4 × 4 board.
79 square cm is the typical surface area of an average brick. *Jennifer Li
The 80th Day of the Year:
There are 80 four-digit primes which are concatenations of two-digit primes. (3137 is one example, can you find the rest?) *Prime Curios!
80 in Roman Numerals is not suitable for minors, LXXX,
The Pareto principle (sometimes called the 80-20 rule) says that, for many events, roughly 80% of the effects come from 20% of the causes, ie, \( \approx 80\% \) of the accidents are caused by 20% of the drivers.
\(n*2^{n-1} \) gives the number of edges (segments) in a n-dimensional cube, and in the 5th dimension, (went there once in a dream) there are 80 edges, 5*24
(It also has eighty two-dimensional square faces.)
And 80 is the smallest number diminished by taking its sum of letters (writing out its English name and adding the letters using a=1, b=2, c=3, ...) *Tanya Khovanova
In 1719 Paul Halcke showed that the product of the aliquot divisors of 80 equals the fourth power of 80. The only year numbers for which this is true is 48 and 80.
80 and 86 combine to form the largest four digit vampire number, 6880. Note 80 x 86 = 6880 and the same four digits are used in both sides of the equality.
80 is the smallest integer n such that both n and n+1 are products of at least 4 primes.*Prime Curios
80 is a semiperfect number, since adding up some subsets of its divisors 1 + 4 + 5 + 10 + 20 + 40 gives 80.
80 is the largest natural number n such that all prime factors of n and n+1 are smaller or equal to the prime digit 5.
80 is palindromic in bases 3, 6, and 9 , and a Repdigit in base 3 and base 9.
The 81st Day of the Year:
There are many numbers for which if you raise the sum of the digits to some power you get the original number. 512 for instance, (5+1 + 2) ^ 3 = 8^3 = 512. For 2401 we can have (2+4+0+1)^4 = 9^4 = 2401. For year dates, the only such numbers that work are 1, and 81. 81 is the largest known number such that the square of the sum of its digits is equal to the number. ( 8 + 1) ^2 = 9^2 = 81.
Student's are reminded that 8 x 10 + 1 is 81 = 9^2, an example of a beautiful mathematical truth that 8 x T + 1 is a square for any triangular number.
The smallest 10 digit pandigital number is 1023456789, 81 or 34 is a factor. The other two factors are both four digit numbers. Can you find the smallest, which is prime? ;-}
81 is one of only three non-trivial numbers for which the sum of the digits * the reversal of the sum yields the original number (8+1 = 9; 9*9 = 81). The other two are the famous Hardy-Ramanujan taxicab # 1729, which is the smallest number which is the sum of two positive cubes in two ways.(1+7+2+9 = 19; 19*91 = 1729), and 1458 (1+4+5+8 = 18; 18*81=1458) which is also unique for being the maximum determinant possible for a 11x11 matrix with only ones and zeros. The Hardy-Ramanujan number's properties were first noted by Frénicle de Bessy in 1657(without mention of a taxicab).That is, he knew it was the sum of two cubes in two ways, not sure if he knew the sum of the digits property above... anyone?
"A dozen, a gross and a score,
Plus three times the square root of four,
Divided by seven,
Plus five times eleven,
Is nine squared, and not a bit more. "
John Saxon.
(12+ 144 + 20 + 3*sqrt(4)) /7 + 5 *11 = 9^2 = 81.
80 and 81 are the smallest integer pair of consecutive numbers such that both are products of at least 4 primes.*Prime Curios
and 80 and 81 are the largest integer pair such that all prime factors of the two are smaller than or equal to the prime digit 5.
81 is the smallest square (and only known) such that n*2n-1 is prime *Prime Curios
There are 81 Full House primes, with the most advantageous being 18181 and 81181 (where 1 is regarded as the Ace.) Supposedly the famous frontier hero, Wild Bill Hickock, died by being shot from behind in a poker game. His hand was a supposedly two pairs, with Aces and Eights and is often called the "dead man's hand". A full house is three of one card and a pair of another.
The decimal expansion of the reciprocal of 81 is \( \overline{ .012345679}.... \) omitting only the 8. This is true of the reciprocal of (b-1)<sup>2</sup> in any base b leaving out only the value b-2 in the repeating period. For example, in base 5, the reciprocal of 16 (31<sub>5</sub> ) is \( \overline{.0124...} \)
If you look into the palm of your left hand with your fingers extended parallel to the ground, you will see the Arabic numeral for eight near the center of your palm, and the numeral for one just above it.
81 is the third smallest number where the sum of its divisors is a perfect square. \(1 + 3 + 9 + 27 + 81 = 11^2 = 121\) There are only three year dates (to my knowledge) for which the sum of the divisors is a square. They all three occur in this MathFacts page, 66, 70, and 81. 66 and 70 even have the same total, 144. The largest of the three, 81, has the smallest sum.
80 is a semiperfect number, since adding up some subsets of its divisors 1 + 4 + 5 + 10 + 20 + 40 gives 80.
80 is the largest natural number n such that all prime factors of n and n+1 are smaller or equal to the prime digit 5.
80 is palindromic in bases 3, 6, and 9 , and a Repdigit in base 3 and base 9.
The 81st Day of the Year:
There are many numbers for which if you raise the sum of the digits to some power you get the original number. 512 for instance, (5+1 + 2) ^ 3 = 8^3 = 512. For 2401 we can have (2+4+0+1)^4 = 9^4 = 2401. For year dates, the only such numbers that work are 1, and 81. 81 is the largest known number such that the square of the sum of its digits is equal to the number. ( 8 + 1) ^2 = 9^2 = 81.
Student's are reminded that 8 x 10 + 1 is 81 = 9^2, an example of a beautiful mathematical truth that 8 x T + 1 is a square for any triangular number.
The smallest 10 digit pandigital number is 1023456789, 81 or 34 is a factor. The other two factors are both four digit numbers. Can you find the smallest, which is prime? ;-}
81 is one of only three non-trivial numbers for which the sum of the digits * the reversal of the sum yields the original number (8+1 = 9; 9*9 = 81). The other two are the famous Hardy-Ramanujan taxicab # 1729, which is the smallest number which is the sum of two positive cubes in two ways.(1+7+2+9 = 19; 19*91 = 1729), and 1458 (1+4+5+8 = 18; 18*81=1458) which is also unique for being the maximum determinant possible for a 11x11 matrix with only ones and zeros. The Hardy-Ramanujan number's properties were first noted by Frénicle de Bessy in 1657(without mention of a taxicab).That is, he knew it was the sum of two cubes in two ways, not sure if he knew the sum of the digits property above... anyone?
"A dozen, a gross and a score,
Plus three times the square root of four,
Divided by seven,
Plus five times eleven,
Is nine squared, and not a bit more. "
John Saxon.
(12+ 144 + 20 + 3*sqrt(4)) /7 + 5 *11 = 9^2 = 81.
80 and 81 are the smallest integer pair of consecutive numbers such that both are products of at least 4 primes.*Prime Curios
and 80 and 81 are the largest integer pair such that all prime factors of the two are smaller than or equal to the prime digit 5.
81 is the smallest square (and only known) such that n*2n-1 is prime *Prime Curios
There are 81 Full House primes, with the most advantageous being 18181 and 81181 (where 1 is regarded as the Ace.) Supposedly the famous frontier hero, Wild Bill Hickock, died by being shot from behind in a poker game. His hand was a supposedly two pairs, with Aces and Eights and is often called the "dead man's hand". A full house is three of one card and a pair of another.
The decimal expansion of the reciprocal of 81 is \( \overline{ .012345679}.... \) omitting only the 8. This is true of the reciprocal of (b-1)<sup>2</sup> in any base b leaving out only the value b-2 in the repeating period. For example, in base 5, the reciprocal of 16 (31<sub>5</sub> ) is \( \overline{.0124...} \)
If you look into the palm of your left hand with your fingers extended parallel to the ground, you will see the Arabic numeral for eight near the center of your palm, and the numeral for one just above it.
 |
81 is the third smallest number where the sum of its divisors is a perfect square. \(1 + 3 + 9 + 27 + 81 = 11^2 = 121\) There are only three year dates (to my knowledge) for which the sum of the divisors is a square. They all three occur in this MathFacts page, 66, 70, and 81. 66 and 70 even have the same total, 144. The largest of the three, 81, has the smallest sum.
The 82nd Day of the Year:
82 is the sum of the 10th(8+2) prime and the 16th(8x2) prime. It is the smallest number with this property. Can you find the next?
82 is a happy number. Take the sum of the square of the digits, repeat on the result, and you eventually arrive at 1.
82 is the number of different ways you can arrange 6 regular hexagons by joining their adjacent sides:
82 can be written as : The sum of Fibonacci numbers, 82 = 1 + 5 + 21 + 55 The sum of consecutive integers, 82= 19 + 20 + 21 + 22 and as the sum of squares 82= 12 + 92 *What's Special About This Number
Start writing the numbers backward from 82 to 1, the concatenated number, 8281807978...4321 is Prime. *Fermat's Library
82 is a palindrome in base 3(1001) and in base 9 (101) (compare to 80 which is a palindrome in both 3 and 9, as well as 6).
82 is a companion Pell Number."In mathematics, the Pell numbers are an infinite sequence of integers, known since ancient times, that comprise the denominators of the closest rational approximations to the square root of 2. This sequence of approximations begins
11, 32, 75, 1712, and 4129, so the sequence of Pell numbers begins with 1, 2, 5, 12, and 29. The numerators of the same sequence of approximations are half the companion Pell numbers or Pell–Lucas numbers; these numbers form a second infinite sequence that begins with 2, 6, 14, 34, and 82."*Wik
Both integer sequences are formed by multiplying twice the last member and adding the one before that, so the companion number 82 = 2*34+14. The associated denominator, or Pell number, 29=2*17 + 7.
82 is a palindrome in base 3(1001) and in base 9 (101) (compare to 80 which is a palindrome in both 3 and 9, as well as 6).
82 is a companion Pell Number."In mathematics, the Pell numbers are an infinite sequence of integers, known since ancient times, that comprise the denominators of the closest rational approximations to the square root of 2. This sequence of approximations begins
11, 32, 75, 1712, and 4129, so the sequence of Pell numbers begins with 1, 2, 5, 12, and 29. The numerators of the same sequence of approximations are half the companion Pell numbers or Pell–Lucas numbers; these numbers form a second infinite sequence that begins with 2, 6, 14, 34, and 82."*Wik
Both integer sequences are formed by multiplying twice the last member and adding the one before that, so the companion number 82 = 2*34+14. The associated denominator, or Pell number, 29=2*17 + 7.
Physicist Otto Stern was nominated for the Nobel Prize on a total of 82 occasions, ultimately receiving the 1943 Physics Prize.
Among his nominators were Albert Einstein, Wolfgang Pauli, Max Planck and Werner Heisenberg.
The 83rd Day of the Year
83 is the smallest prime whose square, 6889, is a strobogrammatic number.
83 is the sum of the squares of the first three consecutive odd primes (3^2 + 5^2 + 7^2).
One of my Mathematical idols, Paul Erdos, died at age 83. I heard about it when one of my advanced math students announced, 'Mr Ballew, you know that Math guy you always talk about; I heard he died last night."
83 is the smallest prime number which is the sum of a prime number of consecutive prime numbers in a prime number of different ways, i.e., 23 + 29 + 31 = 11 + 13 + 17 + 19 + 23. *Prime Curios (Whew! say that three times in a hurry)
The smallest prime with a digit sum of 83 is 3999998999.
83 is The number of permutations of the 10 distinct digits taken 9 at a time that are perfect squares. These range from 101242 = 102495376 to 303842 = 923187456.*Prime Curios
Stewart's cube, shown below, is a graph with 8 vertices and 12 edges. Each edge is assigned a "weight" of unique prime numbers, and the total weight of the three edges meeting at each vertex is 83.
As far as I know this is the first graph found with these properties (unique prime edges and common total). I would like information on which "Stewart" this is named for and when. There is a more recent discovery by Austin Buchanan that has all prime edges and a smaller weight of 77 at each vertex.
83 is a prime number of the form 4n-1 so it can not be expressed as the sum of two squares.
And I just found out that in the Jewish faith, when you reach the age of 83, you can celebrate a 2nd Bar Mitzvah.
"The TI-83 series is a series of graphing calculators manufactured by Texas Instruments. The original TI-83 is itself an upgraded version of the TI-82. Released in 1996, it was one of the most popular graphing calculators for students. In addition to the functions present on normal scientific calculators, the TI-83 includes many features, including function graphing, polar/parametric/sequence graphing modes, statistics, trigonometric, and algebraic functions, along with many useful applications. Although it does not include as many calculus functions, applications and programs can be downloaded from certain websites, or written on the calculator." Wik.
The 84th Day of the Year:
with nine points equally placed around a circle there are 84 different triangles using three of these points as vertices. Are any of them right triangles?
And Jim Wilder hit the trifecta today with :
\(84 = 2^5 + 3^3 + 5^2 \)
\(84 = 2^2 + 4^2 + 8^2 \) and
\( 84 = 1^3 + 1^3 +1^3 + 3^3 + 3^3 + 3^3 =3^3+3\)
And 84 is the sum of three consecutive powers of four \(4^1 + 4^2 + 4^3 = 84\)
84 is the only number that is spelled with ten letters that are all different.
84 is the sum of the first seven triangular numbers, making it the 7th Tetrahedral number.
84 is the smallest number that can be expressed as the sum of three distinct primes raised to prime exponents, 2^5 + 3^3 + 5^2 = 84
84 is also the smallest number that can be expressed as the sum of two primes in 8 different ways. 5+79 is one, the rest are on you.
84 can also be written in four different ways as the sum of four primes, with any three of them summing to a prime. 5 + 13 + 23 + 43 is one of them, *Prime Curios
Little is known of the life of Diophantus, but this problem, supposedly on his tomb, will reveal his age.
The 85th Day of the Year:
85 is the largest number for which the sum of 12 + 22 + 32 + 42 +...+n2= 1+2+3+4+.... +M for some n,M, can you find that M? 85 is the largest such n, with a total sum of squares of 208,335; but can you find some solutions n,M that are smaller? (Reminder for students, the sums of first n consecutive squares are called pyramidal numbers, the sums of the first n integers are called triangular numbers.)
And a bonus I found at the Prime Curios web site, (8511 - 85)/11 ± 1 are twin primes.
85, with 86 and 87 are the second smallest three consecutive numbers such all three are products of two primes. *Don S McDonald
85 is the fourth Hoax number of the year. Yesterday was the third. A Hoax number is a number with the sum of it's digits equal to the sum the digits of it's unique prime factors.
There are 85 five-digit primes that begin with 85.
85 is the sum of consecutive integers, and the difference of their squares \(42+43= 43^2 - 42^2 = 85\),
85 is the ONLY known Smith Number(sum of its digits is same as the sum of the digits of its prime factorization), whose aliquot sum(sum of all prime numbers less than n) is equal to \( \pi(n)\) (The number of primes less than, or equal to n)
85 can be expressed as the sum of two squares in two different ways, 92 + 2 2 = 72 + 62 =85. It is the smallest such number with all squares greater than one.
85 is the length of the hypotenuse in four Pythagorean Triangles. @igor_goldshtein gave the legs, 13 & 84, 36 & 77, 40 & 75, and 51 & 68.
The only composite number resulting from the sum of three double-digit consecutive emirps, 17, 31, 37. Note that the concatenation in order of these emirps, i.e., 173137 is prime *Prime Curios
85 is a palindrome in base 2 (1010101) and a palindrome and a repdigit in base 4 (1111) (85=1+4+16+64)
The 86th Day of the Year
86 is conjectured to be the largest number n such that 2n (in decimal) doesn't contain a 0. *Tanya Khovanova, Number Gossip
The 86th prime is 443, and 4433 = 86,938,307. There is no other two digit n, such that the nth prime starts with n.
86 is the sum of four consecutive integers, 86= 20 + 21 + 22 + 23 and of four consecutive squares,
85, with 86 and 87 are the second smallest three consecutive numbers such all three are products of two primes. *Don S McDonald
86= 32 + 42 + 52 + 62 This is a Truncated Pyramidal number, calculating the sum of the squares from n, to 2n. There are only five such year days, 5, 29, 86, 190 and 355.
The multiplicative persistence of a number is the number of times the iteration of finding the product of the digits takes to reach a one digit number. For 86, with persistence of three, we produce 8*6= 48, 4*8 = 32, and 3*2 = 6.... and 48+32+6 = 86. (how frequently does that occur?)
There are 86 abundant numbers(the sum of the proper divisors is greater than the number) in a non-leap year, but 86 is not one of them. All the abundant year days are even numbers. The smallest odd abundant number is 945.
80 and 86 combine to form the largest four digit vampire number, 6880. Note 80 x 86 = 6880 and the same four digits are used in both sides of the equality.
The 83rd Day of the Year
83 is the smallest prime whose square, 6889, is a strobogrammatic number.
83 is the sum of the squares of the first three consecutive odd primes (3^2 + 5^2 + 7^2).
One of my Mathematical idols, Paul Erdos, died at age 83. I heard about it when one of my advanced math students announced, 'Mr Ballew, you know that Math guy you always talk about; I heard he died last night."
83 is the smallest prime number which is the sum of a prime number of consecutive prime numbers in a prime number of different ways, i.e., 23 + 29 + 31 = 11 + 13 + 17 + 19 + 23. *Prime Curios (Whew! say that three times in a hurry)
The smallest prime with a digit sum of 83 is 3999998999.
83 is The number of permutations of the 10 distinct digits taken 9 at a time that are perfect squares. These range from 101242 = 102495376 to 303842 = 923187456.*Prime Curios
Stewart's cube, shown below, is a graph with 8 vertices and 12 edges. Each edge is assigned a "weight" of unique prime numbers, and the total weight of the three edges meeting at each vertex is 83.
 |
| *John D Cook |
83 is a prime number of the form 4n-1 so it can not be expressed as the sum of two squares.
And I just found out that in the Jewish faith, when you reach the age of 83, you can celebrate a 2nd Bar Mitzvah.
"The TI-83 series is a series of graphing calculators manufactured by Texas Instruments. The original TI-83 is itself an upgraded version of the TI-82. Released in 1996, it was one of the most popular graphing calculators for students. In addition to the functions present on normal scientific calculators, the TI-83 includes many features, including function graphing, polar/parametric/sequence graphing modes, statistics, trigonometric, and algebraic functions, along with many useful applications. Although it does not include as many calculus functions, applications and programs can be downloaded from certain websites, or written on the calculator." Wik.
The 84th Day of the Year:
with nine points equally placed around a circle there are 84 different triangles using three of these points as vertices. Are any of them right triangles?
And Jim Wilder hit the trifecta today with :
\(84 = 2^5 + 3^3 + 5^2 \)
\(84 = 2^2 + 4^2 + 8^2 \) and
\( 84 = 1^3 + 1^3 +1^3 + 3^3 + 3^3 + 3^3 =3^3+3\)
And 84 is the sum of three consecutive powers of four \(4^1 + 4^2 + 4^3 = 84\)
84 is the only number that is spelled with ten letters that are all different.
84 is the sum of the first seven triangular numbers, making it the 7th Tetrahedral number.
84 is the smallest number that can be expressed as the sum of three distinct primes raised to prime exponents, 2^5 + 3^3 + 5^2 = 84
84 is also the smallest number that can be expressed as the sum of two primes in 8 different ways. 5+79 is one, the rest are on you.
84 can also be written in four different ways as the sum of four primes, with any three of them summing to a prime. 5 + 13 + 23 + 43 is one of them, *Prime Curios
Little is known of the life of Diophantus, but this problem, supposedly on his tomb, will reveal his age.
84 is a Hoax number, the sum of it's digits is the same as the sum the digits of it's unique prime factors. It is the third year day which is a hoax number. \( 84 = 2^2 x 3 x 7 \) . So unique prime factors are 2, 3, and 7 with a sum of 12. 8+4 = 12 also. Tomorrow will be the fourth.
A hepteract is a seven-dimensional hypercube with 84 penteract 5-faces.
And 84 is still, I believe, the largest number of times anyone has been nominated for the Noble Prize and never won even once. During the 1901-1950 period, Arnold Sommerfeld was nominated for the Nobel Prize 84 times, more than any other physicist (including Otto Stern,who got nominated 81 times), but he never received the award. His PhD students also earned more Nobel prizes in physics than any other supervisor’s,ever. *Wik
Eighty Four is a census-designated place in Somerset, North Strabane, North Bethlehem and South Strabane townships in Washington County, Pennsylvania, United States. It lies approximately 25 miles (40 km) southwest of Pittsburgh and is in the Pittsburgh metropolitan area. The population was 657 at the 2010 census.
The 85th Day of the Year:
85 is the largest number for which the sum of 12 + 22 + 32 + 42 +...+n2= 1+2+3+4+.... +M for some n,M, can you find that M? 85 is the largest such n, with a total sum of squares of 208,335; but can you find some solutions n,M that are smaller? (Reminder for students, the sums of first n consecutive squares are called pyramidal numbers, the sums of the first n integers are called triangular numbers.)
And a bonus I found at the Prime Curios web site, (8511 - 85)/11 ± 1 are twin primes.
85, with 86 and 87 are the second smallest three consecutive numbers such all three are products of two primes. *Don S McDonald
85 is the fourth Hoax number of the year. Yesterday was the third. A Hoax number is a number with the sum of it's digits equal to the sum the digits of it's unique prime factors.
There are 85 five-digit primes that begin with 85.
85 is the sum of consecutive integers, and the difference of their squares \(42+43= 43^2 - 42^2 = 85\),
85 is the ONLY known Smith Number(sum of its digits is same as the sum of the digits of its prime factorization), whose aliquot sum(sum of all prime numbers less than n) is equal to \( \pi(n)\) (The number of primes less than, or equal to n)
85 can be expressed as the sum of two squares in two different ways, 92 + 2 2 = 72 + 62 =85. It is the smallest such number with all squares greater than one.
85 is the length of the hypotenuse in four Pythagorean Triangles. @igor_goldshtein gave the legs, 13 & 84, 36 & 77, 40 & 75, and 51 & 68.
The only composite number resulting from the sum of three double-digit consecutive emirps, 17, 31, 37. Note that the concatenation in order of these emirps, i.e., 173137 is prime *Prime Curios
85 is a palindrome in base 2 (1010101) and a palindrome and a repdigit in base 4 (1111) (85=1+4+16+64)
The 86th Day of the Year
86 is conjectured to be the largest number n such that 2n (in decimal) doesn't contain a 0. *Tanya Khovanova, Number Gossip
The 86th prime is 443, and 4433 = 86,938,307. There is no other two digit n, such that the nth prime starts with n.
86 is the sum of four consecutive integers, 86= 20 + 21 + 22 + 23 and of four consecutive squares,
85, with 86 and 87 are the second smallest three consecutive numbers such all three are products of two primes. *Don S McDonald
86= 32 + 42 + 52 + 62 This is a Truncated Pyramidal number, calculating the sum of the squares from n, to 2n. There are only five such year days, 5, 29, 86, 190 and 355.
The multiplicative persistence of a number is the number of times the iteration of finding the product of the digits takes to reach a one digit number. For 86, with persistence of three, we produce 8*6= 48, 4*8 = 32, and 3*2 = 6.... and 48+32+6 = 86. (how frequently does that occur?)
There are 86 abundant numbers(the sum of the proper divisors is greater than the number) in a non-leap year, but 86 is not one of them. All the abundant year days are even numbers. The smallest odd abundant number is 945.
80 and 86 combine to form the largest four digit vampire number, 6880. Note 80 x 86 = 6880 and the same four digits are used in both sides of the equality.
86 in base 6 is a repdigit, and thus a palindrome (222) that makes it equal to twice the digits of the beast number raised to consecutive power, 86 = 2* (6^0 + 6^1 + 6^2)
Kentucky Highway 86 is only a fraction of a mile greater than 86/2. It runs from Union Star to US 62 near Cecillia.
The 87th Day of the Year:
87 is the sum of the squares of the first four primes is 87. \(87 = 2^2 + 3^2 + 5^2 + 7^2 \)
87 = 3 * 29, \(87^2 + 3^2 + 29^2 and 87^2 - 3^2 - 29^2 \)are both primes
Among Australian cricket players, it seems, 87 is an unlucky score and is referred to as "the devil's number", supposedly because it is 13 runs short of 100.
87 is the third consecutive day that is semiprime (the product of two primes), 85, with 86 and 87 are the second smallest three consecutive numbers such all three are products of two primes. *Don S McDonald
And 87 is, of course, the number of years between the signing of the U.S. Declaration of Independence and the Battle of Gettysburg, immortalized in Abraham Lincoln's Gettysburg Address with the phrase "fourscore and seven years ago..."
87 is the largest number that yields a prime when any of the one-digit primes 2, 5 or 7 is inserted between any two digits. The only other such number is 27 (and trivially, the 1 digit numbers). *Prime Curios
5! - 4! - 3! - 2! - 1! = 87. Remember the old puzzle of making numbers with four 4's. What numbers could you make with the first five factorials using only the four basic arithmetic functions between them
The 88th Day of the year:
882 = 7744, it is one of only 5 numbers known whose square has no isolated digits. (Can you find the others?) [Thanks to Danny Whittaker @nemoyatpeace for a correction on this.] I find it beautiful that a
two digit repeating number, has a square that is a concatenation of two such numbers.
Any number that ends in 88 will have a square ending in 44. The only numbers whose squares end in double numbers must end in 12, 38, 62, or 88, and they all end in 44. (OK, 38 ends in triple 4)
There are only 88 narcissistic numbers in base ten, (an n-digit number that is the sum of the nth power of its digits, 153=13 + 53 + 33
88 is also a chance to introduce a new word (It was new to me). 88 is strobogrammatic, a number that is the same when it is rotated 180o about its center... 69 is another example. (Not everyone holds to these rules, even me) If they make a different number when rotated, they are called invertible (89 becomes 68 for example). *Prime Curios
And with millions (billions?) of stars in the sky, did you ever wonder how many constellations there are? Well, according to the Internationals Astronomical Union, there are 88.
And if you chat with Chinese friends, the cool way to say bye-bye is with 88, from Mandarin for 88, "bā ba".
Not too far from my home near Possum Trot, Ky, there is a little place called Eighty-eight, Kentucky. One strory of the naming (there could be as many as 88 of them) is that the town was named in 1860 by Dabnie Nunnally, the community's first postmaster. He had little faith in the legibility of his handwriting, and thought that using numbers would solve the problem. He then reached into his pocket and came up with 88 cents.
In the 1948 presidential election, the community reported 88 votes for Truman and 88 votes for Dewey, which earned it a spot in Ripley's Believe It or Not.
And expanding the "88 is strobogrammatic" theme, INDER JEET TANEJA came up with this beautiful magic square with a constant of 88 that was used in a stamp series in Macao in 2014 and 2015. This image shows the reflections both horizontally and vertically, as well as the 180 degree rotation, each is a magic square.
The stamps had denominations of 1 through 9 pataca and when two sheets were printed you could do your own Luo Shu magic square with the denominations. The Luo Shu itself was featured on the 12 pataca stamp.
88 is called a Refactorable Number, because it is divisible by the number of divisors it has. It's the fifteenth so far this year.
The sum of the first 88 emirps, (primes that are still prime when digit order is reversed, 13 and 31 for example) is 88,000, The 88th emirp is 1831*Prime Curios.
88 is a palindrome in base ten, and also in base 5 (323).
And a good reason to remind students Why 88 can not be expressed as the sum of two squares. Any number that has a factor of the form 4n-1 (for 88 that's the 11) that has an odd exponent (like 1) is not the sum of two squares.
88 and 945 are the smallest abundant numbers that share no common divisors. 88 is the 19th abundant number and like all the numbers before it, is even. (45 is the smallest odd abundant number, following 231 even numbers. 945 has prime divisors of 3, 5, and 7 but 88 is the smallest abundant number that has none of these.
There are only 88 narcissistic numbers in base ten, (an n-digit number that is the sum of the nth power of its digits, 153=13 + 53 + 33
88 is also a chance to introduce a new word (It was new to me). 88 is strobogrammatic, a number that is the same when it is rotated 180o about its center... 69 is another example. (Not everyone holds to these rules, even me) If they make a different number when rotated, they are called invertible (89 becomes 68 for example). *Prime Curios
And with millions (billions?) of stars in the sky, did you ever wonder how many constellations there are? Well, according to the Internationals Astronomical Union, there are 88.
Currently, 14 men and women, 9 birds, two insects, 19 land animals, 10 water creatures, two centaurs, one head of hair, a serpent, a dragon, a flying horse, a river and 29 inanimate objects are represented in the night sky (the total comes to more than 88 because some constellations include more than one creature.)
88 is called a Refactorable Number, because it is divisible by the number of divisors it has. It's the fifteenth so far this year.
The sum of the first 88 emirps, (primes that are still prime when digit order is reversed, 13 and 31 for example) is 88,000, The 88th emirp is 1831*Prime Curios.
88 is a palindrome in base ten, and also in base 5 (323).
And a good reason to remind students Why 88 can not be expressed as the sum of two squares. Any number that has a factor of the form 4n-1 (for 88 that's the 11) that has an odd exponent (like 1) is not the sum of two squares.
88 and 945 are the smallest abundant numbers that share no common divisors. 88 is the 19th abundant number and like all the numbers before it, is even. (45 is the smallest odd abundant number, following 231 even numbers. 945 has prime divisors of 3, 5, and 7 but 88 is the smallest abundant number that has none of these.
In the standard English counting system, every single number after EIGHTY-EIGHT has an N in its name. *HT to @HaggardHawks
An Interesting pattern for 88,
9*9+7=88
98*9+6=888
987*9+5=8888
9876*9+4=88888
And it continues .. even into the negative numbers...
987654321*9-1 = 8888888888
The 89th Day of the year:
89 is the fifth Fibonacci prime and the reciprocal of 89 starts out 0.011235... (generating the first five Fibonacci numbers) *Prime Curios It actually generates many more, but the remainder are hidden by the carrying of digits from the two digit Fibonacci numbers. (The next digit, for instance is a 9 instead of an eight because it includes the tens digit of the next Fibonacci number, 13.)
89 is the 11th Fibonacci number, and it is not divisible by any smaller Fibonacci numbers. \( F_m divides F_n \) only if m divides n. Since 89 is the 11th Fibonacci number so it is not divisible by any smaller Fibonacci number. This can help if finding possible factors for numbers are knowing if they are prime. 377 is the 14th Fibonacci number, and 14 is divisible by 7, so 377 is not prime, and is divisible by by F<sub>_7</sub> which is 13. 377 = 13 x 29.
One more note about Fibonacci numbers that ties them to a sequence of hypotenii of right triangles, if you look at Fibonacci numbers beginning with 5; 5, 8, 13, 21, 34, 55, 89... Every other one is the hypotenuse of a Pythagorean triangle. For this case, 39, 80, 89 are the three sides. But if you look at the previous one, 16, 30, 34 you might notice that the sum of these sides is 89, and such is true for each of them.
89 is a factor of 2^11 - 1, the smallest factorable Mersenne Number with a prime exponent.
89 is the 24th prime number,
The base of the Statue of Liberty is 89 feet tall.
89 is an invertible number (rotation by 180 degrees produces a different number, 68) Others refer to such rotations that produce another number as Strobogrammatic. Even another term for them is numeric ambigrams. Which ever term you use, it is the sum of 1+8+11+69, four strobogrammatic numbers.
and 89 can be expressed by the first 5 integers raised to the first 5 Fibonacci numbers: 11 + 25 + 33 + 41+ 52
If you write any integer and sum the square of the digits, and repeat, eventually you get either 1, or 89 (ex: 16; \( 1^2 + 6^2 = 37; 3^2 + 7^2 = 58; 5^2 + 8^2 = 89 \) Numbers that iterate to 1 are called Happy numbers. numbers that do not iterate to 1 eventually fall into the repeating cycle with the eight values 4, 16, 37, 58, 89, 145, 42, and 20.
91^2 - 89 ^2 = 360. *Gary Croft pointed out in a post that if you take the 24 numbers up to 89 that are not divisible by any of 2, 3, or 5 (he uses this set for a very efficient prime sieve) they pair up so that the difference of their squares are multiples of 360 (89^2 - 1^2 = 360 x 22; 83^2 - 7^2 = 360 x 19; ....)
89 = 81 + 92 There are two three digit year dates that share this property, abc = a^1 + b^2 + c^3
An Armstrong (or Pluperfect digital invariant) number is a number that is the sum of its own digits each raised to the power of the number of digits. For example, 371 is an Armstrong number since \(3^3+7^3+1^3 = 371\). There are exactly 89 such numbers, including two with 39 digits. (115,132,219,018,763,992,565,095,597,973,522,401 is the largest) (Armstrong numbers are named for Michael F. Armstrong who named them for himself as part of an assignment to his class in Fortran Programming at the University of Rochester \)
89 is the smallest prime (indeed the smallest positive integer) whose square (7921) and cube (704969) are likewise prime upon reversal. *Prime Curios
And from our strange measures category, A Wiffle, also referred to as a WAM for Wiffle (ball) Assisted Measurement, is equal to a sphere 89 millimeters (3.5 inches) in diameter – the size of a Wiffle ball, a perforated, light-weight plastic ball frequently used by marine biologists as a size reference in photos to measure corals and other objects. The spherical shape makes it omnidirectional and perfect for taking a speedy measurement, and the open design also allows it to avoid being crushed by water pressure. Wiffle balls are a much cheaper alternative to using two reference lasers, which often pass straight through gaps in thin corals. A scientist on the research vessel EV Nautilus is credited with pioneering the technique *Wik
The sum of all the prime numbers up to and including 89 is 963. If you eliminate the single even prime, 2, the total is 961 = 31^2. This is the smallest such sum of primes for which this is true.
The concatenation of all odd primes starting from 89 and counting in reverse is prime.*Prime Curios (so what if it starts with 83?
89 is a Pythagorean Prime, one that is the sum of two squares. 8^2 + 6^2
22 + 33 + 55 + 77 + 1111 + ... + 8989 is prime.
Hellin's law states that twins occur once in 89 births, triplets once in 892 births, and quadruplets once in 893 births, and so forth. This approximation came before the advent of fertility methods. *Prime Curios
89892 = 80802121. 89 is the smallest prime, P so that PP2 is of the form XXYY, *Prime Curios
89^2 - 2 = 7919, the 1000th prime, so there are exactly 1000 primes between 1 and 892
89 is a palindrome in base 8 (131)
How about some sums of sequential primes raised to their own power....that are prime!!!
From the clever Tweets of Srinivasa Raghava K \( 2^2 + 3^3 = 13 \) and
\(2^2 + 3^3 + 5^5 + 7^7 = 826699\) also prime, and
\(2^2 + 3^3 + \dots + 89^{89} \) is BIG... and Prime
Oklahoma City, Ok. was founded in the Land Run of 89, when property in the Indian Nation was opened to white settlers.
Double 89 and add 1, you get a prime. Keep doing it and you'll get a sequence of six such primes. Primes p for which 2p + 1 are also prime are called Sophie Germain primes, after a great female mathematician.
US 89 is called the National Parks Hwy, and runs, almost literally, through Yellowstone Natl Park, and Links it to six more.
The 90th day of the year;
90 is the only number that is the sum of its digits plus the sum of the squares of its digits. (Is there any interesting distinction to the rest of the numbers for which this sum is more (or less) than the original number?)
\( \frac{90^3 - 1}{90 - 1} \) is a Mersenne prime.
90 = 3^2 + 9^2 = 3^2 + 3^4
90 is a Harshad (Joy Giver) number since 90 is divisible by the sum of its digits
90 is the smallest number having 6 representations as a sum of four positive squares
90 is the number of degrees in a right angle. Moreover, as a compass direction, 90 degrees corresponds to east. Which reminds me of a fun math joke:"The number you have dialed is imaginary. Please rotate you phone by 90 degrees and dial again."
And 90 is the sum of the first 9 consecutive even numbers, the sum of consecutive integers in two different ways, the sum of two consecutive primes, and of six consecutive primes(in two distinct ways), and the sum of five consecutive squares. (all proofs left to the reader.)
(903 - 1)/(90 - 1) is a Mersenne prime. *Prime Curios The bases in Major League Baseball are 90 feet apart.
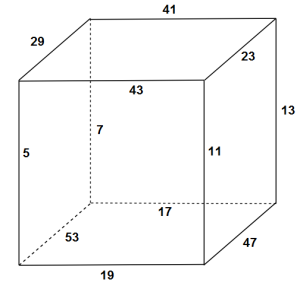
No comments:
Post a Comment