Not sure where I learned that between any two perfect squares, there is never exactly 1 prime.
And a comment on the Aperiodical Blog points out that, "If we write dates as 8 digit numbers yyyymmdd, then 2018 had 18 prime dates. 2019 will have 19 prime dates, and 2021 will have 21." How many does 2023 have?
2020 is also a Harshad number (it's divisible by the sum of its digits in base ten). It is the 406th of them, so there are only about 20% of (smallish) numbers that are.The last such year was 2016, and the next will be in 2022, but then we get four in a row, 2023, 2024, 2025 also are all divisible by the sum of their digits.
The word "harshad" comes from the Sanskrit harṣa (joy) + da (give), meaning joy-giver. *Wik, I hope this is a Joyous mathematical year for all of you.
1, 25, 49 is the smallest arithmetic progression of three squares that I have ever found. 4, 100, and 196 come next . Is there one starting with nine? It is proven that an arithmetic progression of four squares in not possible.
The continued fraction for the Golden Ratio contains only ones. 
Day 2
The 2nd day of the year; the smallest prime, and the only even prime.
Euler's beautiful theorem for polyhedra shows that , the number of vertices plus the number of faces minus the number of edges will equal two. V + F - E = 2 For example, a cube has 8 vertices, 6 faces, and 12 edges, and 8 + 6 - 12 = 2.
The sum of the reciprocals of the triangular numbers is 2, 2 = 1/1 + 1/3 + 1/6 + 1/10 + ...
And perhaps the most beautiful way to define perfect numbers: Let n be a perfect number. Then the reciprocals of n's divisors sum to 2 *Algebra Fact @AlgebraFact (For example, 28 is a perfect number, it's divisors are 1, 2, 4, 7, 14, and 28. So 1/1 + 1/2 + 1/4 + 1/7 + 1/14 + 1/28 = 2
If 2n+1 is prime, and n > 0, it can be shown that n must be a power of two. However the converse was incorrectly conjectured by Fermat in 1650 and disproved by Euler in 1732 showing the counter-example F(5) = 232+1 = 4294967297 = 641×6700417
Day 3 The 3rd day of the year; 3 is the only prime followed by a square, and every positive integer is the sum of at most 3 triangular numbers. (Can every triangular number greater than 1 be written as the sum of exactly three triangular numbers?) The smallest Prime Knot has 3 crossings.
(Am I wrong in thinking that each time you remove the outside radical and each
outside term and coefficient, the total increases by one?)
If 2n+1 is prime, and n > 0, it can be shown that n must be a power of two. However the converse was incorrectly conjectured by Fermat in 1650 and disproved by Euler in 1732 showing the counter-example F(5) = 232+1 = 4294967297 = 641×6700417
Day 3 The 3rd day of the year; 3 is the only prime followed by a square, and every positive integer is the sum of at most 3 triangular numbers. (Can every triangular number greater than 1 be written as the sum of exactly three triangular numbers?) The smallest Prime Knot has 3 crossings.
Ramanujan gave this infinite iterated radical, @ AnalysisFact
3 is the only triangular number which is prime...the singular intersection of two infinite sets of integers.
Day 4
The 4th day of the year; it is the smallest composite number.
Every positive integer is the sum of at most 4 squares.
There are 44 numbers in a year which can not be expressed with less than four squares. The smallest is 7, the largest is 359
Brocard conjectured that there are at least four primes between the squares of any two consecutive primes, with the exception of 2 and 3.
For any number k, real or complex, \( 4 = k^2 - (k+1)^2 - (k+2)^2 + (k+3)^2 \)
The fourth dimension has more regular "solids" than other dimensions. Euclid, in the Elements, proves that there are exactly five regular solids in three dimensions. Schläfli proves that there are exactly six regular solids in four dimensions, There are no higher dimensions with more. There are five regular polyhedra in three space, the Platonic solids. There are six regular 4-space polyhedra. Five of the 4-space polyhedra are analogs of the Platonic solids in 3-space, but there is also a 24-cell, with 24 octahedral faces w/o analog to the Platonic solids. Beyond 4-space, the number of regular polyhedra is always three.
The product of pi and the square root of phi( the golden ratio) is equal to 4, ok not exactly, but close. It is appx 3.99616
In the Kepler triangle with sides
consider:the circle that circumscribes it,
and a square with side equal to the middle-sized edge of the triangle.
Day 5
The fifth day of the year; five is the number of Platonic Solids.
Five is also the smallest number of queens needed to attack every square on a standard chess board. (can you demonstrate such a board ?)
In a tweet to @Wayword I suggested two terms for "multiples of five", particular years ending with 0 or five. The terms were semi-decennial and quinquevalent. (Interested in others).
Day 4
The 4th day of the year; it is the smallest composite number.
Every positive integer is the sum of at most 4 squares.
There are 44 numbers in a year which can not be expressed with less than four squares. The smallest is 7, the largest is 359
Brocard conjectured that there are at least four primes between the squares of any two consecutive primes, with the exception of 2 and 3.
For any number k, real or complex, \( 4 = k^2 - (k+1)^2 - (k+2)^2 + (k+3)^2 \)
The fourth dimension has more regular "solids" than other dimensions. Euclid, in the Elements, proves that there are exactly five regular solids in three dimensions. Schläfli proves that there are exactly six regular solids in four dimensions, There are no higher dimensions with more. There are five regular polyhedra in three space, the Platonic solids. There are six regular 4-space polyhedra. Five of the 4-space polyhedra are analogs of the Platonic solids in 3-space, but there is also a 24-cell, with 24 octahedral faces w/o analog to the Platonic solids. Beyond 4-space, the number of regular polyhedra is always three.
The product of pi and the square root of phi( the golden ratio) is equal to 4, ok not exactly, but close. It is appx 3.99616
In the Kepler triangle with sides
consider:the circle that circumscribes it,
and a square with side equal to the middle-sized edge of the triangle.
Then the perimeters of the square (
) and the circle (
) coincide up to an error less than 0.1% *Wik
The four color theorem for planes says that a map can be colored in no more that four colors with no adjacent regions the same color. On a Mobius strip, the magic number is six, and on a torus, it is seven.
) and the circle () coincide up to an error less than 0.1% *WikThe four color theorem for planes says that a map can be colored in no more that four colors with no adjacent regions the same color. On a Mobius strip, the magic number is six, and on a torus, it is seven.
A 3,4,5 triangle is a Heronian triangle with consecutive integer sides, and integer area. There are only four such triplets where the sides are year dates. Each of them have an even integer for their base, and so their altitude is an integer also. I call them Sang-Heronian triangles after the earliest study I know about them by Edward Sang of Edinburgh, Scotland in 1864
Day 5
The fifth day of the year; five is the number of Platonic Solids.
 |
| *David Darling, info |
Five is also the smallest number of queens needed to attack every square on a standard chess board. (can you demonstrate such a board ?)
In a tweet to @Wayword I suggested two terms for "multiples of five", particular years ending with 0 or five. The terms were semi-decennial and quinquevalent. (Interested in others).
There are five equable (area and perimeter "equal" and integer side lengths) triangles . All of them have area & perimeter divisible by six. (I'm willing to learn why if you know) [W. A. Whitworth and D. Biddle proved this in 1904] the ones with side lengths (5,12,13), (6,8,10), (6,25,29), (7,15,20), and (9,10,17).
The sum of the first five integers raised to their own power, is prime, \(1^1 + 2^2 + 3^3 + 4^4 + 5^5 = 3413 \) (and so is the sum of the first six)
One of math's perplexing mysteries. A sphere in five dimensional space has a larger volume (\( \frac{8 \pi ^2}{15} \) ) than in any other dimension for a unit radius. From two dimensions up to five the volume increases, then decreases forever after.
In 1845, Gabriel Lame proved a remarkable theorem involving the number 5. "The number of steps (i.e., divisions) in an application of the Euclidean algorithm never exceeds 5 times the number of (decimal) digits in the lesser." Donald Knuth (1969) extended this to show that, this was related to the Fibonacci numbers (and \( \sqrt{5} \) ).
and from Jim Wilder : 1084 is the smallest integer whose spelling, one thousand eighty-four, contains the 5 vowels (a, e, i, o, u) in order.
A prime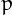 
is a Pierpont prime if it can be written as 
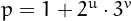, for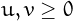 
. 5=1+2^2 * 3^0 These numbers are related to the constructable regular polygons
Day 6
The sixth day of the year;
The sum of the first five integers raised to their own power, is prime, and so is the sum of the first six \(1^1 + 2^2 + 3^3 + 4^4 + 5^5 +6^6 = 50069 \)
six is the smallest perfect number, and Lord Karl Voldevive@Karl4MarioMugan pointed out that, "All other known perfect numbers end in 44 in base 6 as do all powers of ten greater than ten."
"One would be hard put to find a set of whole numbers with a</b>
\( \pi^4 + \pi^5 = e^6 \) almost, (403.428775... vrs 403.428793...)
Note that 6 is a perfect number AND a triangular number, and the same is true for every perfect number.
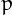is a Pierpont prime if it can be written as 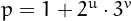, for . 5=1+2^2 * 3^0 These numbers are related to the constructable regular polygonsDay 6
The sixth day of the year;
The sum of the first five integers raised to their own power, is prime, and so is the sum of the first six \(1^1 + 2^2 + 3^3 + 4^4 + 5^5 +6^6 = 50069 \)
six is the smallest perfect number, and Lord Karl Voldevive@Karl4MarioMugan pointed out that, "All other known perfect numbers end in 44 in base 6 as do all powers of ten greater than ten."
"One would be hard put to find a set of whole numbers with a</b>
more fascinating history and more elegant properties surrounded
by greater depths of mystery—and more totally useless—than the perfect numbers"
.—Martin Gardner
\( \pi^4 + \pi^5 = e^6 \) almost, (403.428775... vrs 403.428793...)
Note that 6 is a perfect number AND a triangular number, and the same is true for every perfect number.
The four color theorem for planes says that a map can be colored in no more that four colors with no adjacent regions the same color. On a Mobius strip, the magic number is six, and on a torus, it is seven.
The Feynman point is a sequence of six 9s that begins at the 762nd decimal place of the decimal representation of π. It is named after physicist Richard Feynman, who once stated during a lecture he would like to memorize the digits of π until that point, so he could recite them and quip "nine nine nine nine nine nine and so on", suggesting, in a tongue-in-cheek manner, that π is rational.
There are five equable (area and perimeter "equal" and integer side lengths) triangles . All of them have area & perimeter divisible by six. (I'm willing to learn why if you know) [W. A. Whitworth and D. Biddle proved this in 1904] the ones with side lengths (5,12,13), (6,8,10), (6,25,29), (7,15,20), and (9,10,17).
And from 1089 
A Devilish trigonometry equivalence sin(666o = cos (6*6*6o)
Every prime greater than three is either one more, or one less than a multiple of six.
6 + 1, 6 ⋅ 66 + 1, 6 ⋅ 66 ⋅ 666 + 1, 6 ⋅ 66 ⋅ 666 ⋅ 6666 ⋅ 66666 ⋅ 666666 + 1 and 6 ⋅ 66 ⋅ 666 ⋅ 6666 ⋅ 66666 ⋅ 666666 ⋅ 6666666 + 1 are prime numbers. *NumberSense
Six is an unincorporated community in McDowell County, West Virginia, United States. Six is located on West Virginia Route 16 5 miles (8.0 km) southwest of Welch.
Day 7
The 7th day of the year;
you can double 7! to get the exact number of minutes in a week (7 days).
Mario Livio pointed out that The sum of the squares of the first seven primes was 666, the supposed number of the beast from Revelations. \( 666=2^2+3^2+5^2+7^2+11^2+13^2+17^2 \) . May I add that seems devilishly clever.
Ever wonder if 7 cylinders could be arranged so that each touched the other six? Yep(but eight is up to you)
In the digital expansion of pi, 7 is the last (non-zero) single digit to occur, showing up in the 13th place after the decimal point. (If you randomly drew from nine distinct objects with replacement, How long would it take to get them all, on average?)
And The smallest prime of length 7 containing only the digits 7 and 8 is palindromic: 7778777 *@pickover
Jim Wilder @wilderlab sent this one: 7⁴ = 2401 = (2+4+0+1)⁴
The four color theorem for planes says that a map can be colored in no more that four colors with no adjacent regions the same color. On a Mobius strip, the magic number is six, and on a torus, it is seven.
A Devilish trigonometry equivalence sin(666o = cos (6*6*6o)
Every prime greater than three is either one more, or one less than a multiple of six.
6 + 1, 6 ⋅ 66 + 1, 6 ⋅ 66 ⋅ 666 + 1, 6 ⋅ 66 ⋅ 666 ⋅ 6666 ⋅ 66666 ⋅ 666666 + 1 and 6 ⋅ 66 ⋅ 666 ⋅ 6666 ⋅ 66666 ⋅ 666666 ⋅ 6666666 + 1 are prime numbers. *NumberSense
Six is an unincorporated community in McDowell County, West Virginia, United States. Six is located on West Virginia Route 16 5 miles (8.0 km) southwest of Welch.
Day 7
The 7th day of the year;
you can double 7! to get the exact number of minutes in a week (7 days).
Mario Livio pointed out that The sum of the squares of the first seven primes was 666, the supposed number of the beast from Revelations. \( 666=2^2+3^2+5^2+7^2+11^2+13^2+17^2 \) . May I add that seems devilishly clever.
Ever wonder if 7 cylinders could be arranged so that each touched the other six? Yep(but eight is up to you)
And The smallest prime of length 7 containing only the digits 7 and 8 is palindromic: 7778777 *@pickover
Jim Wilder @wilderlab sent this one: 7⁴ = 2401 = (2+4+0+1)⁴
The four color theorem for planes says that a map can be colored in no more that four colors with no adjacent regions the same color. On a Mobius strip, the magic number is six, and on a torus, it is seven.
There are an infinite number of primes, and an infinite number of cubes, but the only incidence of a prime followed by a cube, is 7 followed by eight. Can your students show why there is not even one example of a case where cube is followed by a prime?
And just for the seventh day of 2016, 2016 is the sum of cubes of seven consecutive integers \(2016 = 3^3 + 4^3 + 5^3 + 6^3 + 7^3 + 8^3 + 9^3 \)
The 8th day of the year;
the well known Fibonacci sequence has only two cubes, one and eight
The square root of the first 8 digits of pi, (31415926) ^(1/2) is nearly an integer (5604.991) So far no square root of the first n digits of pi has been found which is an integer. Whether one exists is still an open question. HT Fermat's Library
And another from the same source (but pointed out by Douglas Hofstadter) is that the sum of the reciprocals of the first 8 integers rounded to three decimal places is a good approximation for e, 2.718
I post here the method I taught students to remember e to 16 digits. Simply remember President Andrew Jackson, He was elected for two terms, and was the 7th president of the US, and he was elected first in 1828, but because he served two terms we repeat that, and he loved equilateral triangles, so add on 45, 90, 45...... 2.718281828459045. (so the equilateral triangle thing is probably not actually true, but it is a good mnemonic,)
There are 8! minutes in four weeks, say February in a non leap year.
8 and 9 (\( 2^3 , 3^2 \) are the only consecutive powers of integers. The result, \(x^p - y^q=1\) has only one solution for integers x, y both greater than 1) conjectured in 1842 by Eugène Catalan, was proved in 2002 by Preda Mihăilescu.
An interesting approximation for eight from @fermatslibrary \( \frac {987654321}{123456789} = 8.0000000729...\)
8 3 = 512 and 5+1+2 = 8; (Any other cubes with this property?)
I found a post by Ben Vitale that relates the number eight to the digital root of twin primes. Other than the pair three and five (3x5 = 15, 1+5 = 6),
According to a tweet from @HaggardHawks "cabbaged" is the longest dictionary word that can be spelled using musical notes. (It's British slang for wasted, by alcohol or drug)
Eight was an unincorporated community located in McDowell County, West Virginia. (Six is an unincorporated community located in the same county. Six is known to be named for a mine. Anyone know about Eight?) The Eight post office closed in 1936.
Day 9
The 9th day of the year;
of all the odd numbers in the Fibonacci sequence, none has a factor of nine. (students might search for the smallest odd prime number that is not a factor of any of the Fibonacci numbers)
8 and 9 (\( 2^3 , 3^2 \) are the only consecutive powers of integers. The result, \( x^y-y^x \) has only one solution for x, y both greater than 1) conjectured in 1842 by Eugène Catalan, was proved in 2002 by Preda Mihăilescu.
If you wrote $ \pi$, e, and $\phi $ one under another, they all have a 9 in the 13th digit.
And *Jim Wilder@wilderlab tweeted, "9 can be written upside down and read the same in binary: 1001, or when written as shown in the photo."
And from Cliff Pickover @Pickover, the square of the nine digit rep unit produces an interesting number, 111,111,1112; = 12345678987654321
I found a post by Ben Vitale that relates the number eight to the digital root of twin primes. Other than the pair three and five (3x5 = 15, 1+5 = 6),
5 * 7 = 35, 3 + 5 = 8, 11 * 13 = 143, 1 + 4 + 3 = 8, 17 * 19 = 323, 3 + 2 + 3 = 8, 29 * 31 = 899, 8 + 9 + 9 = 26, 2 + 6 = 8, 41 * 43 = 1763 1 + 7 + 6 + 3 = 17, 1 + 7 = 8 . 59 * 61 = 3599, 3 + 5 + 9 + 9 = 26, 2 + 6 = 8, 71 * 73 = 5183, 5 + 1 + 8 + 3 = 17, 1 + 7 = 8. 101 * 103 = 10403, 1 + 0 + 4 + 0 + 3 = 8, ( to help prove this, read the day 6 facts carefully.)The only known number to appear 8 times in Pascal's Arithmetic Triangle, is the palindrome 3003. It is conjectured that, a) no number can appear more than eight times and b) 3003 is the only number that will appear eight times. *John D. Cook
According to a tweet from @HaggardHawks "cabbaged" is the longest dictionary word that can be spelled using musical notes. (It's British slang for wasted, by alcohol or drug)
The Kissing Number, the number of spheres that can be placed around a central sphere so that they all are touching it, for the eighth dimension is 240. Beyond the fourth dimension, only the eighth and twenty-fourth are known exactly. The 24th dimension is the highest dimension for which the exact "kissing number", is known. For the 24th dimension, the "kissing number is 196,560.
Cube root of 8^3 =512 is interesting, add the digits of 512. Could it happen again, try 4913^3 = 17; or 26^3 = 17576, and 27^3 = 17576. *Hat tip to Srinivasa Raghava K and to *Expert_Says, who pointed out there are only 6 natural numbers which satisfy this property. (can you guess which two I left out?)
Day 9
The 9th day of the year;
of all the odd numbers in the Fibonacci sequence, none has a factor of nine. (students might search for the smallest odd prime number that is not a factor of any of the Fibonacci numbers)
8 and 9 (\( 2^3 , 3^2 \) are the only consecutive powers of integers. The result, \( x^y-y^x \) has only one solution for x, y both greater than 1) conjectured in 1842 by Eugène Catalan, was proved in 2002 by Preda Mihăilescu.
If you wrote $ \pi$, e, and $\phi $ one under another, they all have a 9 in the 13th digit.
And *Jim Wilder@wilderlab tweeted, "9 can be written upside down and read the same in binary: 1001, or when written as shown in the photo."
And from Cliff Pickover @Pickover, the square of the nine digit rep unit produces an interesting number, 111,111,1112; = 12345678987654321
One of the favorite numbers of Mathematicians is 1729, the famous taxicab number when Hardy went to visit Ramanujan in the hospital. Many students know it is the smallest number that is the sum of two positive cubes in two ways. 12^3 + 1^3 is and easy one, and the second is 10^3 + 9^3.
But don't stop there. Nine also figures in the next .smallest number that is the sum of two positive cubes in two ways, 4104 = 2^3 + 16^3 = 15^3 + 9^3
Day 10
The 10th day of the year; The ten decimal digits 0,1,2,3,4,5,6,7,8,9 can form 3265920 ten digit pandigital numbers. (How many of them are prime?)
10! seconds is exactly six weeks.
and 10! = 6! x 7! There are no other examples of n! = a! x b! except cases in which n itself is a factorial number. (See day 120)
10 balls can be arranged in the plane as a triangle, and in space as a tetrahedron.
Ramanujan said this exotic formula came to him in a dream:
There is also only one number that is spelled with ten distinct letters, eighty-four.
At Haggard Hawks I learned about a Finnish unit of measurement for the distance at which a dog bark could be heard. It was called a peninkulma . " As a unit of measurement, that being said, the peninkulma was originally defined not using the fairly imprecise yardstick of a dog’s long-distance bark, but as a unit of length equal to 5 virsta—a measurement (based on the even older Russian verst) equal to around two-thirds of a mile. That made the original peninkulma equivalent to roughly 3.3 miles, but in the early seventeenth century it was redefined as 10 virsta—or 6.6 miles. Then, when Finland adopted the metric system in 1880, the peninkulma was redefined to 10 kilometres—or 6.2 miles. "
Day 11
The 11th day of the year;
11 is the only prime comprising an even number of identical digits. (Can you find a prime which is comprised of an odd number of identical digits?)
To my knowledge, 11 is the only number that can be expressed as the sum of three distinct digits so that their reciprocals add up to one. 11 = 2 + 3 + 6 and \( \frac{1}{2} + \frac{1}{3}+\frac{1}{6}=1 \)
Not only is 11 + 2 = 12 + 1, but "eleven plus two" is an anagram of "twelve plus one." *Cliff Pickover @pickover
It is commonly known that you can find two consecutive numbers greater than one whose squares sum to a perfect square, (3,4) (20,21) for example are well known consecutive legs of Pythagorean Triples. But less well known is that the next smallest ; n for which the sum of n consecutive squares is a perfect square is 11, for which \( \sum_{k=18}^{28} k^2 = 77^2 \)
Almost an integer, Sin(11) = -.9999902...
Multiplicative persistence is the number of times you have to iterate the product of the digits of n to get a one digit number. It seems that you'll never need more than 11 iterations to make it work, at least, up to 10233 we know that's true. (for example the multiplicative persistence of 77 is four. 7x7=49, 4x9=36, 3x6=18, 1x8 = 1... and btw, there is no day of the year that has a higher multiplicative persistence than that.)
Day 12
The 12th day of the year;
12 is the smallest abundant number (number whose proper factors add up to more than the number itself).
It is also the largest number of spheres that may be in contact with a given sphere in 3-D (This is not trivial, Newton couldn't prove it). See Kissing Number.
Behold the Oreo, it's a tasty treat and a duodecimal sensation. Each has 12 dashes, 12 dots, and 12 flowers around the periphery. Observe... dip in the milk... ahhhhh
And for chess buffs, it takes 12 knights to attack/occupy every square on chessboard. And there are 12 ways for 8 queens to be placed on a chess board so that none attacks another.
And Fermat was wrong, at least for the 12th dimension. 1782¹² + 1841¹² = 1922¹² (Well, almost; and from the 1995 Halloween "Treehouse of Horror" series on The Simpsons). *Simon Singh
The 12 letter word "tattarrattat" is the longest palindrome in the Oxford English Dictionary, coined by James Joyce in Ulysses for a knock on the door
There is only one number that is spelled with twelve different letters. 5000
*Pi Guy@grey_matter In 1913 R. D. Carmichael proved his conjecture that for any Fibonacci Number F(n), with n greater than 12, has at least one prime factor that is not a factor of any earlier Fibonacci number.
Paul Halcke noted in 1719, that 12 was one of three numbers for which the sum of the aliquot divisors sum to its square. 20 and 44 are the other two.
12 figures in the famous story of Ramanujan's Taxicab number. The story says that when G H Hardy went to visit Ramanujan in the hospital, he commented that the number of his taxi, 1729, was singularly uninteresting. Ramanujan replied that it was very interesting number as it was the smallest number which was the sum of two cubes in two ways. This was not, as some stories suggest, an immediate recognition of some mathematical fact. Ramanujan's mathematical notebooks had numerous explorations of nearly cubic numbers, numbers like 1729=12^3+1. And a lover of number theory like Ramanujan would immediately recognized that 1729 = 1000 + 729 = 10^3 + 9^3. Shortly after I arrived at Misawa AFB in Japan to begin teaching for the DODDS schools, I went to the base post office to get a post office box. The clerk had no idea why I was so excited when he gave me my box number.....Yep, 1729.
If you don't count trivial one-digit numbers, there are 12 year days which are divisible by the sum of their digits, and the product of their digits, and the smallest of them is..... 12! 12 is divisible by 1+2 and by 1x2. There are only three two digit numbers with this property. Can you find them?
12 is also a Lynch-Bell number. These numbers must have all digits distinct, and each digit is a divisor of the number. 12 is the smallest such example for the year. Stephen Lynch and Andrew Bell are Brisbane surgeons who contributed to the identification of this sequence.
Day 13 The 13th day of the year; there are 13 Archimedian Solids.
(different from the Platonic solids, which have only one type of polygon meeting in identical vertices)
If you wrote \( \pi\), e, and \(\phi \) one under another, the first digit they are all alike is the 13th digit, a nine in each number.
The sum of the first n digits of pi equals a prime year day only 11 times. It is even more rare that the number of digits summed to get a prime, is itself prime. The smallest of these is when the first 13 digits are summed to get the prime 61. No other prime number of digits of pi will sum to a prime year day.
Day 13 The 13th day of the year; there are 13 Archimedian Solids.
 |
| *kidsBritanica.com |
(different from the Platonic solids, which have only one type of polygon meeting in identical vertices)
If you wrote \( \pi\), e, and \(\phi \) one under another, the first digit they are all alike is the 13th digit, a nine in each number.
The sum of the first n digits of pi equals a prime year day only 11 times. It is even more rare that the number of digits summed to get a prime, is itself prime. The smallest of these is when the first 13 digits are summed to get the prime 61. No other prime number of digits of pi will sum to a prime year day.
The 13th palindromic prime is 373 and has a digit sum of 13. 13 is smallest n for which digit sum of nth palindromic .
Another 13 palindrome, The longest word in the English language that is a palindrome in Morse code is .. -. - .-. .- -. ... .. --. . -. -.-. . (translation left to the reader, if your coding is rusty try copy and paste to http://morsecode.scphillips.com/translator.html)
And 13 is the smallest prime that remains prime when iterated five times through the function f(p) = 2p+5. f(13)=31, f(31)= 67, f(67)=129, f(129) = 263, f(263)=531.
Day 14
The 14th day of the year; there are exactly the same number of composite and prime numbers less than fourteen. There is no larger number for which that is true.
By selecting one of + or - between each number, there are 14 solutions to \( \pm 1 \pm 2 \pm 3 \pm 4 \pm 5 \pm 6 \pm 7 \pm 8 = 0\) *Derek Orr
A sonnet is a 14 line poem.
Like the 3,4,5 triangle, the 13, 14, 15 triangle is a Heronian triangle with consecutive integer sides, and integer area. There are only four such triplets where the sides are year dates (366 or smaller). Each of them have an even integer for their base, and so their altitude is an integer also. This one has an altitude of 12, and like all the non-right angled ones, the altitude and right triangles formed by it are Primitive Pythagorean Triangles, this one is composed of a 5, 12, 13 sharing it's 12 leg with a 9, 12, 15. I call them Sang-Heronian triangles after the earliest study I know about them by Edward Sang of Edinburgh, Scotland in 1864
A cuboctahedron is a solid with 14 sides. It has six squares and eight equilateral triangles. It is one of the Archimedian Solids mentioned on Day 13.
Mystics assert that 14 is the number of forgetfulness, and perhaps they are right, almost no one remembers Franklin Pierce, the 14th President of the US. Hat tip to *DearKidLoveMom
Day 15
The 15th day of the year; Everyone knows Ramanujan’s famous taxicab number, 1729, which is the smallest number that is the sum pf two positive cubes in two ways, but what’s Next. ..,...
2^3+ 16^3= 15^3 +9^3=4104
15 is the maximum number of pieces that can be produced from a cylindrical cake with four planar slices. These are called "cake numbers" and the first four are 2, 4, 8, and 15. What comes next?
The first known magic square dates back to about 650BCE in China. This is when the great king Yu found a sea turtle with a nine pattern square on its back with patterns of dots forming the Lo Shu pattern with each row, column, and diagonal adding up to 15. All normal 3x3 magic squares are derived from this pattern.
 |
| Wikipedia |
The 15 digit word "Saippuakauppias" is Finnish for "soap dealer," and one of the longest single-word palindromes in everyday use. *Cliff Pickover @pickover (This is the longest single word palindrome in the world that is in everyday use) (The English 12-letter word tattarrattat, is the longest palindrome in the Oxford English Dictionary, was coined by James Joyce in Ulysses for a knock on the door)
The alternating factorial, \(\pm 15!\) = 15! - 14! + 13! - 12! + ,,, + 3! - 2! + 1! = 1220280710981 a prime number. *Fermat's Library.
The Fifteen Puzzle was the Rubick's Cube of it's day. Popularized (but not invented) by American puzzle master Sam Loyd. Get your own
or read the story here, from a modern day puzzle master,
"Just a Jiffy" is a unit of time. It is defined, according to Robert McNees as the time it takes light to travel a distance of 1 fermi (or one femtometer or \( 10 ^{-15}\) meters) Which he says is \(3 x 10^{-24}\).
Day 16
The 16th day of the year; 16 is the only number that can be written as ab = ba when a and b are not equal.
16 and its next smaller square, 9, form a square when added or multiplied: 16+9=25, 16x9=144
16 is the smallest number which is the sum of two distinct primes in two ways, 16 = 3 + 13 = 5 + 11
Jim Wilder pointed out that 1616 ends in 1616 , 18446744073709551616
Day 17
The 17th day of the year; there are 17 prime partitions of 17. No other number is equal to its number of prime partitions. (for example, 7 has 3 prime partitions, 7, 3+2+2, and 5+2)
And 17 is the ONLY PRIME that is equal to the sum of four consecutive primes, 17 = 2 + 3 + 5 + 7, and also It is the only known prime that is equal to the sum of digits of its cube *Mario Livio @Mario_Livio (173 = 4913, and 4 + 9 + 1 + 3 = 17). But wait, also the only prime that is the average of two consecutive Fibonacci numbers. ... (Ok, that would be 13 and 21... now the only way Fibonacci numbers can have an intege (*Mario Livio @Mario_Livior value is if they are both odd [there are no consecutive even Fibonacci numbers}, and all the even Fibonacci numbers are twice the average of the two previous values... so there can be no Fibonacci number after 34 which is twice a prime) It is interesting that there are lots of odd prime Fibonacci numbers, 2, 3, 5, 13, 89, 233, 1597, 28657, for example , Sloane's A005478, and each of them has a prime index (except three, which is f4).
None of the odd Fibonacci numbers is divisible by 17, but then they are not divisible by 19, or 23, so not sure if that is unusual or not; more to discover.
If you write out the numbers from 1 to 5000 in English (e.g., THREE THOUSAND EIGHT HUNDRED SEVENTY-THREE), it turns out that 17 is the only one that has a unique number of characters (nine).
(Spaces and hyphens count as characters) .
Trigonometric functions of \( \frac{npi}{17} \) for n an integer can be expressed in terms of sums, products, and finite root extractions because 17 is a Fermat prime. This makes the heptadecagon constructible, as first proved by Gauss.
Jim Wilder@wilderlab pointed out: 17 = 2³ + 3² 17 = 3⁴ - 4³ 17³ = (4+9+1+3)³ = 4913
With any number of points less than 17, it is possible to color all the segments between them with two colors without any triangle having all three sides of the same color. With 17 or more, it is not possible.
cutie, 17 = 1 - 2 - 3 - 4 - 5 + 6 + 7 + 8 + 9
The sum of the squares of the first seven primes (all primes up to 17) is 666, the "Number of the Beast." \(2^2 + 3^2 + 5^2 + 7^2 + 11^2 + 13^2 + 17^2 = 666 \)
17 mph is an unusual speed limit, but on the campus of Hampshire College in Amherst all the speed limit signs have been changed from 15 to 17 miles per hour to honor retired mathematics professor David Kelly. Kelly spent his career fascinated by the number 17. There is at least two others in the US, at Mountain View, California and Fiesta Mall in Mesa, Az. For those interested, this site lists 17 (of course) interesting facts about 17 from the Professor.
 |
| David Kelly at Hampshire College *MSN.COM |
Day 18
The 18th day of the year; there is only one number (289=172) for which the sum of its proper divisors is 18.
(can you figure out which numbers can never appear as the sum of the proper divisors?)
Harshad /"Joy-giver" Numbers were created by Indian Mathematician D. R. Kaprekar, to apply to any number that is divisible by the sum of its digits. 18 is a Harshad number since 18 is divisible by the sum of 1+8. One well known famous number, the Hardy-Ramanujan Taxi-cab number, 1729 is also a Harshad number, since 1729 is divisible by 1+7+2+9 = 19, and almost too nicely, the other factor is 91, the reverse of 19. See, can you feel the Joy it gave you?
You can make a three by three square with a magic sum of any multiple of 3. Adding one to each square of the standard Lo Shu pattern gives a magic sum of 18:
5 10 3
4 6 8
9 2 7
And a one followed by Nineteen nines,(19,999,999,999,999,999,999) is the smallest number with additive persistence of four (add the digits, then add the digits of the result and continue until you get a single digit. The total number of times you added the digits is the "persistence")
183=(5+8+3+2)3=5832*jim wilder @wilderlab
And speaking of powers of 18, 18^3 = 5832 and 18^4 = 104976, together they use all ten decimal digits once each. Smallest (only?) such number.*Ben Vitale
Chris Maslanka@ChrisMaslanka pointed out that 18 is involved in another "smallest" number,
Day 20 The 20th day of the year; 20 is the smallest number that cannot be either prefixed or followed by one digit to form a prime. (What is next smallest?)
The 20th palindromic prime (929) has a digit sum of 20. *jim wilder @wilderlab ... There is no larger nth prime palindrome for which digit sum = n less than \(10^7\) *Derek Orr & *David @InfinitelyManic
\( e^\pi - \pi = 20 \) Well, almost, it's 19.999099979..., (The number \( e^\pi \) is often called Gelfond's constant, after the mathematician Aleksandr Gelfond, who proved that it was transcendental.
20 is involved in a challenge by Fermat in 1647 to "find a cube, that when increased by the sum of its aliquot parts, is a square." The cube, was \(7^3 = 343\) , and the sum of the cube and its aliquot divisors \( 7^3 + 1+ 7 + 7^2 = 400 = 20^2\)
Paul Halcke observed, in 1719, that 20 was one of three (12 and 44 are the other two) numbers for which the product of their aliquote divisors equaled their square. Can you find others?
Both the dodecahedron and the icosahedron have 20 faces. They may be positioned at a common center so that in the center of each of the 12 faces of the dodecahedron is one of the 12 vertices of the icosahedron, in the center of each of the 20 faces of the icosahedron is one of the 20 vertices of the dodecahedron, and the 30 edges of the dodecahedron and the 30 edges of the icosahedron cross each other at right angles at their midpoints.
Every day from Jan 20 to Jan 29 in 2021 will be a palindrome on m/dd/yy
And a one followed by Nineteen nines,(19,999,999,999,999,999,999) is the smallest number with additive persistence of four (add the digits, then add the digits of the result and continue until you get a single digit. The total number of times you added the digits is the "persistence")
183=(5+8+3+2)3=5832*jim wilder @wilderlab
And speaking of powers of 18, 18^3 = 5832 and 18^4 = 104976, together they use all ten decimal digits once each. Smallest (only?) such number.*Ben Vitale
Chris Maslanka@ChrisMaslanka pointed out that 18 is involved in another "smallest" number,
378 = 2 X 3 X 3 X 3 X 7; sum of these prime factors = 18; sum of the digits of 378 is also 18. The smallest multidigit number for which sum of digits = sum of prime factors.
Day 19
The 19th day of the year; 19 is the smallest number n such that nn contains all 10 digits *Number Gossip
19 is also the smallest base ten number that is NOT a palindrome in any base \(2 \leq b \leq 10\) Seems strange that it is the first palindrome (with more than one character) in Roman Numerals XIX.
And more on powers of 19, \( 19^0 + 19^1 + 19^2 + ... +19^{18}\) a total of 19 consecutive powers of 19, is prime. *@Fermat's Library
19 is a factor of 6 of the 8 smallest Taxi-cab numbers (numbers that are the sum of two cubes in two different ways.)
This 19 digit number is a strobogrammatic palindrome prime (rotate it 180 degrees and it still is a palindrome prime ) and 666 in the middle. 1191196166616911911, with a hat tip to INDER JEET TANEJA@IJTANEJA
Speaking of Prime Speed signs, here's two from Lamplighter way on the approach to Northfield Mount Hermon HS in Massachusetts. (HT to @centerofmath)
Day 19
The 19th day of the year; 19 is the smallest number n such that nn contains all 10 digits *Number Gossip
19 is also the smallest base ten number that is NOT a palindrome in any base \(2 \leq b \leq 10\) Seems strange that it is the first palindrome (with more than one character) in Roman Numerals XIX.
And more on powers of 19, \( 19^0 + 19^1 + 19^2 + ... +19^{18}\) a total of 19 consecutive powers of 19, is prime. *@Fermat's Library
19 is a factor of 6 of the 8 smallest Taxi-cab numbers (numbers that are the sum of two cubes in two different ways.)
This 19 digit number is a strobogrammatic palindrome prime (rotate it 180 degrees and it still is a palindrome prime ) and 666 in the middle. 1191196166616911911, with a hat tip to INDER JEET TANEJA@IJTANEJA
Speaking of Prime Speed signs, here's two from Lamplighter way on the approach to Northfield Mount Hermon HS in Massachusetts. (HT to @centerofmath)
Day 20 The 20th day of the year; 20 is the smallest number that cannot be either prefixed or followed by one digit to form a prime. (What is next smallest?)
The 20th palindromic prime (929) has a digit sum of 20. *jim wilder @wilderlab ... There is no larger nth prime palindrome for which digit sum = n less than \(10^7\) *Derek Orr & *David @InfinitelyManic
\( e^\pi - \pi = 20 \) Well, almost, it's 19.999099979..., (The number \( e^\pi \) is often called Gelfond's constant, after the mathematician Aleksandr Gelfond, who proved that it was transcendental.
20 is involved in a challenge by Fermat in 1647 to "find a cube, that when increased by the sum of its aliquot parts, is a square." The cube, was \(7^3 = 343\) , and the sum of the cube and its aliquot divisors \( 7^3 + 1+ 7 + 7^2 = 400 = 20^2\)
Paul Halcke observed, in 1719, that 20 was one of three (12 and 44 are the other two) numbers for which the product of their aliquote divisors equaled their square. Can you find others?
Both the dodecahedron and the icosahedron have 20 faces. They may be positioned at a common center so that in the center of each of the 12 faces of the dodecahedron is one of the 12 vertices of the icosahedron, in the center of each of the 20 faces of the icosahedron is one of the 20 vertices of the dodecahedron, and the 30 edges of the dodecahedron and the 30 edges of the icosahedron cross each other at right angles at their midpoints.
 |
Every day from Jan 20 to Jan 29 in 2021 will be a palindrome on m/dd/yy
*Nationl Museum of Mathematics (Next month a similar event will happen in February, etc for 2023-2029
The first twenty digits of Pi sum to 97. The first twenty-one sum to 103. Both are primes. This is the first two consecutive n, such that the sum of the digits of Pi to that number of digits is prime. The next pair of such consecutive digits of pi are the 106th and 107th digits of Pi.
Day 21
The 21st day of the year; To tile a square out of integer sided squares requires a minimum of 21 squares. (technically, this is true for what are called "simple" squared squares, one where no subset of the squares forms a rectangle or square. See the solution here) (btw: There are no cubed cubes!)
There are 21 possible ways to draw 5 circles that touch all the points on a 5x5 lattice. *gotmath.com
21 repeated twenty-one times, following a 1, forms a smoothly undulating palindromic prime 121212121212121212121212121212121212121.
Blackjack primes are separated by exactly 21 consecutive composite numbers. Note that the pair {1129, 1151} is the smallest example.(Can you find more?) *Prime Curios
Day 22
The 22nd day of the year; 22 is the smallest Hoax number (the sum of its digits is equal to the sum of the digits of its distinct prime factors). Can you find the next? [these sums that Hoax numbers add up to are an interesting study also]. 22 is also called a Smith number. Smith numbers use all the prime factors up to their multiplicity, while hoax numbers use each prime factor only once. See 355 or 364. Many Smith numbers are also hoax numbers. See 121 for the naming of Smith numbers.
Arrange the whole numbers from 1 to 22 into pairs so that the sum of the numbers in each pair is a perfect square. (Turns out that you can't, and 22 is the largest even number for which this is true) * Henri Picciotto@hpicciotto
Extra bonus: 22! has exactly 22 digits. *Mario Livio @Mario_Livio There are only three numbers, n, such that n! is n digits long, 22, 23, and 24.
22 is the smallest number which can be expressed as the sum of two primes in three ways. (Don't just sit there, find the three ways!)
In the 22nd Math Carnival of Denise Gaskins, John Golden offered up a Number Haiku from one of his classes; a number that sounds like Haiku when read, and this one involves 22. 22,220,220. Would love to hear more like this..... send me your Haiku kazu.
Day 23
The 23rd day of the year; 23! is 23 digits long (22, 23, and 24 each solve n! is n digits in length (decimal)).
Day 21
The 21st day of the year; To tile a square out of integer sided squares requires a minimum of 21 squares. (technically, this is true for what are called "simple" squared squares, one where no subset of the squares forms a rectangle or square. See the solution here) (btw: There are no cubed cubes!)
21 repeated twenty-one times, following a 1, forms a smoothly undulating palindromic prime 121212121212121212121212121212121212121.
Blackjack primes are separated by exactly 21 consecutive composite numbers. Note that the pair {1129, 1151} is the smallest example.(Can you find more?) *Prime Curios
Day 22
The 22nd day of the year; 22 is the smallest Hoax number (the sum of its digits is equal to the sum of the digits of its distinct prime factors). Can you find the next? [these sums that Hoax numbers add up to are an interesting study also]. 22 is also called a Smith number. Smith numbers use all the prime factors up to their multiplicity, while hoax numbers use each prime factor only once. See 355 or 364. Many Smith numbers are also hoax numbers. See 121 for the naming of Smith numbers.
Arrange the whole numbers from 1 to 22 into pairs so that the sum of the numbers in each pair is a perfect square. (Turns out that you can't, and 22 is the largest even number for which this is true) * Henri Picciotto@hpicciotto
Extra bonus: 22! has exactly 22 digits. *Mario Livio @Mario_Livio There are only three numbers, n, such that n! is n digits long, 22, 23, and 24.
22 is the smallest number which can be expressed as the sum of two primes in three ways. (Don't just sit there, find the three ways!)
In the 22nd Math Carnival of Denise Gaskins, John Golden offered up a Number Haiku from one of his classes; a number that sounds like Haiku when read, and this one involves 22. 22,220,220. Would love to hear more like this..... send me your Haiku kazu.
Day 23
The 23rd day of the year; 23! is 23 digits long (22, 23, and 24 each solve n! is n digits in length (decimal)).
2 is a prime number.
23 is a prime number.
234, and 2345, and 23456 all are obviously not prime.
234567 looks promising, but alas it is a multiple of three, and 2345678 is surely not prime.
23456789 IS a prime number, and the largest prime number that has consecutive digits.... that means if you go on, 23456789101112.... you will never, ever, ever..... ever find a prime. (Whew, I'm exhausted just thinking about it. HT to @fermatslibrary.
23 is also the answer to the classic Birthday Problem. (How many randomly selected people in a group makes the probability greater than 50% that (at least)two share a common birthdate.)
There are only two values of \( x>0 \) so that \( x^3 + (x+1)^3 +(x+2)^3 \)is a perfect square. The largest is 23. \( 23^3+24^3 + 25^3 = 41616 = 204^2 \) *@BenVitale
decimal # 11111111111111111111111 is prime (23 ones) . *Math Year-Round @MathYearRound
This is, to the best of my knowledge, the largest such string ever to be found prime. All primes less than 100 have been tested and no larger ones found prime. Only known prime repunits are those with two, nineteen, and twenty-three consecutive ones.
23 is also the answer to the classic Birthday Problem. (How many randomly selected people in a group makes the probability greater than 50% that (at least)two share a common birthdate.)
There are only two values of \( x>0 \) so that \( x^3 + (x+1)^3 +(x+2)^3 \)is a perfect square. The largest is 23. \( 23^3+24^3 + 25^3 = 41616 = 204^2 \) *@BenVitale
decimal # 11111111111111111111111 is prime (23 ones) . *Math Year-Round
This is, to the best of my knowledge, the largest such string ever to be found prime. All primes less than 100 have been tested and no larger ones found prime. Only known prime repunits are those with two, nineteen, and twenty-three consecutive ones.
No primes p= 23 (Mod 30) will be part of a twin prime pair. HT *Gary W. Croft
Day 24
The 24th day of the year; 24! (6.2044840173323943936 1023)is almost equal to Avogadro's Number,
(6.022141×10^23).
24 may be the only number in the whole of the integers such that there are four distinct numbers which sum to 24, and whose reciprocals add up to one. 24= 2+4+6+12 and \( \frac{1}{2}+\frac{1}{4}+\frac{1}{6}+\frac{1}{12}=1\)
Also 12 + 22 +...+ 242 = 702 the only pyramidal number that is also a square., that means 24 is the largest n such that the sum of the squares of the first n integers is a square number.
There are five regular polyhedra in three space, the Platonic solids. There are six regular 4-space polyhedra. Five of the 4-space polyhedra are analogs of the Platonic solids in 3-space, but there is also a 24-cell, with 24 octahedral faces w/o analog to the Platonic solids. Beyond 4-space, the number of regular polyhedra is always three.
The 24th dimension is the highest dimension for which the exact "kissing number", the number of spheres that can be placed around a central sphere so that they all are touching it, is known. For the 24th dimension, the "kissing number is 196,560. Beyond the fourth dimension, only the eighth and twenty-fourth are known exactly.
24! has 24 digits. There are only three numbers, n, such that n! is n digits long, 22, 23, and 24.
Paul Halcke discovered in 1719 that the product of the aliquot divisors of 24, equals its cube, \(1*2*3*4*6*8*12 = 13824=24^3\) and that the same fact is true about 40.
"Just a Jiffy" is a unit of time. It is defined, according to Robert McNees as the time it takes light to travel a distance of 1 fermi (or one femtometer or \( 10 ^{-15}\) meters) Which he says is \(3 x 10^{-24}\) sec.
24 is the smallest number which can be expressed as the sum of two primes in three distinct ways. 19+5 = 17+7 = 11+13 = 24
Every prime number, p, greater than 3, p^2-1 is a multiple of 24. When p=5, we get 5^2-1=24. HT to Cye,
24 is the smallest even number expressible as the sum of two primes in three distinct ways. 5 + 19 = 7 + 17 = 11 + 13 = 24
Day 25
The 25th day of the year; 25 is the smallest square that can be written as a sum of 2 squares. (What's the next?)
1, 25, 49 is the smallest arithmetic progression of three squares that I have ever found. 4, 100, and 196 come next . Is there one starting with nine? It is proven that an arithmetic progression of four squares in not possible.
There are 1958 partitions of 25.
The Goldbach representations of 25 using distinct primes are: 2 + 23 = 3 + 5 + 17 = 5 + 7 + 13 = 25.
25 is a palindrome in base 4 (121)
There are 25 primes less than 100. \(25 = 5^2\) and \(2.5 = \frac{5}{2} \) *Math Year-Round @MathYearRound (are there other examples like this?)There are exactly 25 square numbers less than or equal to 1,000,000 that are the sum of twin prime pairs. *prime curios
Everyone knows 25 is the hypotenuse of a Pythagorean right triangle with legs of 7 and 24. A Pythagorean triangle can never have two sides that are squares. When a square occurs as the shorter leg, and interesting pattern occurs:
leg leg hypotenuse
9 40 41
25 312 313
49 1200 1201
81 3280 3281
Day 26
The 26th day of the year; 26 is the smallest non-palindrome with a palindromic square. (676). (What's the next smallest?)
Fermat's sandwich theorem states that 26 is the only number sandwiched between a perfect square number \(5^2=25\) and a perfect cubic number \(3^3 = 27\). According to Singh (1997), after challenging other mathematicians to establish this result while not revealing his own proof, Fermat took particular delight in taunting the English mathematicians Wallis and Digby with their inability to prove the result.*Wolfram Mathworld
When the single digits are raised to 26th power, only 526 contains all ten digits. 526 = 1490116119384765625
Their is a community called Twenty-six in Kentucky. An unincorporated community in Morgan County, the story is told that the community's first postmaster, Martha Rowland, submitted 25 possible community names, and then jotted down "26," which was the year she submitted the list — 1926. The post office was officially established in 1927, and closed in 1957. East of Lexington between Morhead and West Liberty.
Day 27
The 27th day of the year; 273 = 19,683 which has a digit sum of 27. There is no larger number for which the sum of the digits of the cube is equal to the number
. In the 3n+1 or Collatz problem, the sequence for n = 27 takes 111 steps (41 steps through odd numbers), climbing to 9232 before descending to 1. The first starting number to exceed this height is 255.
Of the first 25 Taxi-cab numbers (numbers which are the sum of two cubes in two ways) 27 is the most common digit sum, occurring in seven of the twenty-five. It turns out that all seven of these numbers are also Hashard numbers, divisible by the sum of their digits. In fact, only 14 of the twenty-five are Harshad numbers, and seven of these have digit sum of 27. Three others are divisible by 18, and one by 9. Two of the remaining three (which includes 1729) are divisible by 19, and one is divisible by 36
Day 26
The 26th day of the year; 26 is the smallest non-palindrome with a palindromic square. (676). (What's the next smallest?)
Fermat's sandwich theorem states that 26 is the only number sandwiched between a perfect square number \(5^2=25\) and a perfect cubic number \(3^3 = 27\). According to Singh (1997), after challenging other mathematicians to establish this result while not revealing his own proof, Fermat took particular delight in taunting the English mathematicians Wallis and Digby with their inability to prove the result.*Wolfram Mathworld
When the single digits are raised to 26th power, only 526 contains all ten digits. 526 = 1490116119384765625
Their is a community called Twenty-six in Kentucky. An unincorporated community in Morgan County, the story is told that the community's first postmaster, Martha Rowland, submitted 25 possible community names, and then jotted down "26," which was the year she submitted the list — 1926. The post office was officially established in 1927, and closed in 1957. East of Lexington between Morhead and West Liberty.
Day 27
The 27th day of the year; 273 = 19,683 which has a digit sum of 27. There is no larger number for which the sum of the digits of the cube is equal to the number
. In the 3n+1 or Collatz problem, the sequence for n = 27 takes 111 steps (41 steps through odd numbers), climbing to 9232 before descending to 1. The first starting number to exceed this height is 255.
Of the first 25 Taxi-cab numbers (numbers which are the sum of two cubes in two ways) 27 is the most common digit sum, occurring in seven of the twenty-five. It turns out that all seven of these numbers are also Hashard numbers, divisible by the sum of their digits. In fact, only 14 of the twenty-five are Harshad numbers, and seven of these have digit sum of 27. Three others are divisible by 18, and one by 9. Two of the remaining three (which includes 1729) are divisible by 19, and one is divisible by 36
The reciprocal of 27, 1/27 = .037037037... which would not be at all strange, except, 1/37 = -027027027 Can we call numbers like this, amicable reciprocals? *Cliff Pickover
and Alex Kontorovich found 1/1287 = .000777000777... and yeah, 1/777 = .001287001287...
Balanced letters in the US alphabet are letters whose position in the alphabet are equal distances from the front and back, A and Z, B and Y, etc. Balanced words are words so that the pair of letters equal distance from both ends of the word have the same alphametric sum (a=1, b=2, etc.) . An example is Wizard, where W and D add up to 27, I and R add up to 27 and Z and A add up to 27 .
Can you find another word where the paired positions in the word have the same sum?
For words with an odd number of letters, the center letter alone must be the same as the paired sums of the other letters. One example would be MOB, M + B = O =15.
If you find more of either kind, would love to have you share.
27 is the smallest multi-digit number with the sum of its digits equal to the sum of it's prime factors, 2+7 = 3 +3 +3 Hat Tip to Chow.
27 is the smallest composite number which cannot be expressed as the sum of two primes.
I think it is nice that when you add the integers from 2 to 7, you get 27.... 2 + 3 + 4 + 5 + 6 + 7 = 27
Write down the counting numbers from 2 to 27 concatenated, 234567891011.... 252627. It's a prime number. *K. Srinivasa Raghava. (and may I just say...... WOW!)
Write down the counting numbers from 2 to 27 concatenated, 234567891011.... 252627. It's a prime number. *K. Srinivasa Raghava. (and may I just say...... WOW!)
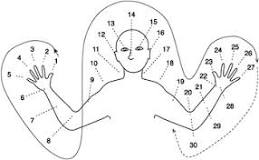
The Oksapmin people of New Guinea have a base-27 counting system. The words for numbers are the words for the 27 body parts they use for counting, starting at the thumb of one hand, going up to the nose, then down the other side of the body to the pinky of the other hand, as shown in the drawing. 'One' is tip^na (thumb), 6 is dopa (wrist), 12 is nata (ear), 16 is tan-nata (ear on the other side), all the way to 27, or tan-h^th^ta (pinky on the other side).
Day 28 The 28th day of the year; 28 is the second perfect number and the last year day that will be perfect; the sum of its proper factors. 28 = 1+2+4+7+14. Like all the perfect numbers after 6, it is the sum of the cubes of consecutive odd numbers, \(28=1^3 + 3^3 \) And like all perfect numbers after 6, when expressed in base 6, it ends in 44.
28 and all perfect numbers (plus some non-perfect numbers) are harmonic divisor numbers, the harmonic mean of their divisors (including the number itself) is an integer. For 28, the harmonic mean of its divisor is 3. That is the index of it's Mersenne prime (2^3 -1) and the same is true for all perfect numbers.
28 is expressible as the sum of first five nonprime numbers, i.e., 1 + 4 + 6 + 8 + 9 = 28.
28 is the number of dominoes in the standard double-6 set. How many in a double-12 set
And a 28-sided polygon is called an icosikaioctagon.
Day 29
The 29th day of the year; 229 = 536870912 a nine-digit number with no digit repeated. Is it possible to create a power of a single digit number that has ten distinct digits?
The digits of 29 appear in one of the most unusual un-mistake I can imagine in numbers, if you inadvertently wrote the exponents of \(2^5 9^2 \) on the same line as the bases you get 2592 which is = \(2^5 9^2 \). It is believed that this is the only such example.
28 is a perfect number, and I think it is interesting that we have proven that if there is ever an odd perfect number it will have at least 29 prime factors, the largest will be greater than 108
There are only two prime day numbers that can be the hypotenuse of a primitive Pythagorean Triangle with consecutive integer legs, 3,4,5; and 20, 21, 29. The next prime hypotenuse for these is 5741. Can you find the legs?***
28 is expressible as the sum of first five nonprime numbers, i.e., 1 + 4 + 6 + 8 + 9 = 28.
28 is the number of dominoes in the standard double-6 set. How many in a double-12 set
And a 28-sided polygon is called an icosikaioctagon.
Day 29
The 29th day of the year; 229 = 536870912 a nine-digit number with no digit repeated. Is it possible to create a power of a single digit number that has ten distinct digits?
The digits of 29 appear in one of the most unusual un-mistake I can imagine in numbers, if you inadvertently wrote the exponents of \(2^5 9^2 \) on the same line as the bases you get 2592 which is = \(2^5 9^2 \). It is believed that this is the only such example.
28 is a perfect number, and I think it is interesting that we have proven that if there is ever an odd perfect number it will have at least 29 prime factors, the largest will be greater than 108
There are only two prime day numbers that can be the hypotenuse of a primitive Pythagorean Triangle with consecutive integer legs, 3,4,5; and 20, 21, 29. The next prime hypotenuse for these is 5741. Can you find the legs?***
And I like this "Euler-like" function from Legendre in 1798, 2n2 + 29 is prime for all n from 0 through 28.
The oldest known mathematical object, a Talley stick, or bone in this case, is the Lebombo bone from southern Africa, and is estimated to be 44,000 years old. It is a Fibula from a baboon that has 29 marked cuts in it and one of the suggested uses was that a was a lunar phase counter. *Wik
Day 30
The 30th day of the year; both the dodecahedron and the icosahedron have 30 edges. They may be positioned at a common center so that in the center of each of the 12 faces of the dodecahedron is one of the 12 vertices of the icosahedron, in the center of each of the 20 faces of the icosahedron is one of the 20 vertices of the dodecahedron, and the 30 edges of the dodecahedron and the 30 edges of the icosahedron cross each other at right angles at their midpoints.
 |
(I find this incredibly wonderful) astounding to me, but 11+22+33...+3030 = 208492413443704093346554910065262730566475781 is prime Republic of Math @republicofmath If there is another prime of this type, it will have over 20025 digits.
7! hours is 30 weeks
and from *@MathYearRound 30 = 2*3*5 (first 3 primes). 30 =\( 1^2+2^2+3^2+4^2 \)(first 4 perfect squares).
30 = 1*1*2*3*5 (first 5 Fibonacci #).
When the iterated sum of the squares of digits of a number produce 1, it is called a Happy Number. If any number is Happy, and permutation of it's digits is also Happy, and inserting any number of zeros also will result in a Happy Number (13 for instance is Happy, since 12 + 22= 10, and 12 + 22= 1, so 31, 103, 301 and 310 are also Happy Numbers.
I have proposed the use of the term Principle Happy numbers for those that do not contain a zero, or any reordering of a previous happy number. That would reduce the above list to the following 30, and makes searches more direct since no descending sequences of digits can exist. 1, 7, 13, 19, 23, 28,44, 49, 68, 79, 129, 133, 139, 167, 188, 226, 236, 239, 338, 356, 367, 368, 379, 446, 469, 478, 556, 566, 888, and899, Note that the last day year which is a principal happy number is Day 356.
30 is the largest integer such that every smaller positive number that is relatively prime to it is a prime number. *Algebra Etc.
A 3x3 magic square with a magic sum of 30 can be found by doubling the entries in the famous Lo Shu triangle
 |
| *Wikipedia |
8 18 4
6 10 14
16 2 12
It can also be done with consecutive digits by adding five to each entry of the basic square
9 14 7
8 10 12
13 6 11
In a card I received for my (80th) birthday on January 24th, I was informed that for every prime number greater than 3, p^2-1 is a multiple of 24. I calculated the first few such multiples and checked with the OEIS. Indeed, this is well known and belongs in your On This Day in Math. Reference: http://oeis.org/A024702.
ReplyDeleteThank you. Yes it should be here, and it will.
Delete