121 is the smallest square that requires five powers of two for a sum.\( 2^6 + 2^5 + 2^4 + 2^3 + 2^0 \) No smaller square needs more than three. The next square year day requiring five will be in the last week of December.
121 will be the largest year day of the form n!+1 which is a square number. Brocard conjectured in 1904 that the only solutions of n! + 1 = m2 are n = 4, 5, and 7. There are no other solutions with
The alternating factorial 5! - 4! + 3! - 2! + 1! = 121. The alternating factorial sequence is prime for n= 3 through 8 (5, 19, 101, 619, 4421, 35899). In spite of this run of consecutive primes, John D Cook checked and found only 15 n values for which the alternating factorial starting with n is prime. 14 are year days, the largest being 160. The one non-year day it turns out uses the same digits as 160, 601.
121 is also the only square of the form 1 + p + p2+ p3 +p4. where p is prime. Find the value of n. Other such squares, if they exist, must exceed 35 digits.
121 is a Smith Number, a composite number for which the sum of its digits is equal to the sum of the digits in its prime factorization. Smith numbers were named by Albert Wilansky of Lehigh University. He noticed the property in the phone number (493-7775) of his brother-in-law Harold Smith: 4937775 = 3 × 5 × 5 × 65837, while 4 + 9 + 3 + 7 + 7 + 7 + 5 = 3 + 5 + 5 + 6 + 5 + 8 + 3 + 7 = 42.
There are 49 Smith numbers below 1000, collect the whole set.
121 is a palindrome in base ten, and also in base 3 (11111), base 7 (232) and base 8(171). No other year day is a base ten palindrome and also palindrome in as many other (2-9) bases.
121 is a palindromic number that is the square of another palindromic number. Several others should be easy to find.
Fermat conjectured that 4 and 121 are the only numbers of the form n^3-4.
You can write 121 as the sum of a prime and its reversal in three different ways. Can you find them?
 |
| *Wikipedia |
Every number greater than 121 is the sum of distinct primes of the form 4n+1.
121 is the smallest composite palindrome for which a permutation of the digits, 211, is prime. *Prime Curios
121 in base 3 is a repdigit (11111), and a palindrome in base ten and base 8 (171), and is 3D in base 36.
On a personal point, M-121 was originally the name of the major east-west highway across Michigan's Upper Peninsula, now US 2. Passing about four miles south of my wife's retreat home near Rexton.
The 122nd day of the year
there are 122 different ways to partition the number 24 into distinct parts. Euler showed that this is the same as the number of ways to partition a number into odd parts. One distinct way would be (12, 6, 3, 2, 1) , five distinct numbers, and one odd way would be (3,3,3,3,3,3,3,3) with eight odd parts, or (21,3) with only two odd parts.
122 ends in the digit two when written in base 3, 4, 5, 6, 8, 10, 12, 15, and 20. How unusual is that?
and 122 is the smallest sum of two non-consecutive factorials of distinct primes (2! + 5!) *Prime Curios
Not sure how unusual this is, but there are no twin primes between 121^2 and 122^2?
The 123rd Day of the Year:
The number formed by the concatenation of odd numbers from 123 down to 1 is prime. (ie 123121119...531 is Prime) *Prime Curios (Who figures stuff like this out???)
Japan Airlines Flight 123, was the world's deadliest single-aircraft accident in history.
And here is an interesting curiosity from the archimedes-lab.org/numbers file: Write down any number (excluding the digit 0): 64861287124425928 Now, count up the number of even and odd digits, and the total number of digits it contains, as follows: 12 | 5 | 17
Then, string those 3 numbers together to make a new number, and perform the same operation on that: 12517 1 | 4 | 5
Keep iterating: 145 1 | 2 | 3 You will always arrive at 123.
123 is the tenth Lucas Number, named for Eduoard Lucas who studied and extended the similar Fibonacci numbers, and was the creator of the fascinating Towers of Hanoi puzzle.
*Srinivasa Raghava K@SrinivasasR1729
There are only two positive integers that are both two more than a perfect square, and two less than a cube, 123 = 11^2 + 2 and 5^3 - 2. The other should be easy to find.
And some of us remember a popular IBM software spreadsheet from the '80s, Lotus 123.
And 123 is the difference of two squares in two different ways, 62² - 61² and 22² - 19². The pattern of both these are explained in Day 111.
The 124th Day of the Year
124 =σ( 1! * 2! * 4!) *Prime Curios (The sigma function of a positive integer n is the sum of the positive divisors of n)
124 is also an Odious number: a number with an odd number of 1's in its binary expansion.(just recently, it occurred to me that it would be more appropriate if an Odious number, had an odd number of "0's")
124 in base two is expressed as 1111100. (Easy to see 31*4 in that)
±1 ± 2 ± 3 ± 4 ± 5 ± 6 ± 7 ± 8 ± 9 ± 10 ± 11 ± 12 = 0 has 124 solutions (collect the whole set) *Math Year-Round @MathYearRound
124 is the sum of eight consecutive primes..... find them children.
In all the infinity of positive integers, there is not one of them whose proper divisors add up to 124; such numbers are called untouchable.
124 in base five is a repdigit, 444, which means it's one less than 5^3 (students new to studying bases should observe that a repdigit k units long in base n, will always be (n^k)-1.
And in case it's not obvious, the digits of 124 form an exponential sequence, called the doubling sequence, 1, 2, 4..
The 124th Day of the Year
124 =σ( 1! * 2! * 4!) *Prime Curios (The sigma function of a positive integer n is the sum of the positive divisors of n)
124 is also an Odious number: a number with an odd number of 1's in its binary expansion.(just recently, it occurred to me that it would be more appropriate if an Odious number, had an odd number of "0's")
124 in base two is expressed as 1111100. (Easy to see 31*4 in that)
±1 ± 2 ± 3 ± 4 ± 5 ± 6 ± 7 ± 8 ± 9 ± 10 ± 11 ± 12 = 0 has 124 solutions (collect the whole set) *Math Year-Round @MathYearRound
124 is the sum of eight consecutive primes..... find them children.
In all the infinity of positive integers, there is not one of them whose proper divisors add up to 124; such numbers are called untouchable.
124 in base five is a repdigit, 444, which means it's one less than 5^3 (students new to studying bases should observe that a repdigit k units long in base n, will always be (n^k)-1.
And in case it's not obvious, the digits of 124 form an exponential sequence, called the doubling sequence, 1, 2, 4..
124 is divisible by four so it is the difference of two squares of numbers that differ by 2, and since 124 / 4 = 31, the numbers must straddle 31, 32² - 30² = 124.
The 125th Day of the Year
125 is a cube, and the sum of distinct squares (and these are distinct PRIMES squared.) There is no smaller value for which this is true. 125 = 53 = 112 + 22 What's the next? It can also be 10^2 + 5^2 .
The 125th Day of the Year
125 is a cube, and the sum of distinct squares (and these are distinct PRIMES squared.) There is no smaller value for which this is true. 125 = 53 = 112 + 22 What's the next? It can also be 10^2 + 5^2 .
Like every perfect cube n^3 can be written as a sequence of consecutive odd numbers. for 5^3 the string of five is the add numbers in the 20's, 21+23+25+27+29
Another way to find the sum is to form n^3 by adding the nth triangular number, T(n) and then n-1 terms with a difference of n. For 25 you get T(5) + (T(5)+5) + (T(5)+10) + (T(5)+15) + (T(5)+20).
5^3 = 15 + 20 + 25 + 30 + 35
125 can also be written as a curious sort of palindrome, 125 = 5(2+1) *Jim Wilder, @wilderlab
Conjectured by Zhi-Wei Sun to be the largest power (53) for which there is no prime between it and the previous power (112). The other prime gaps between powers are in (23, 32), (25, 62) and (52, 33).
125 and 126 are a Ruth Aaron pair of the second kind. In the first kind prime factors are only counted once, in the second kind they are counted as often as they appear, so 5+5+5 = 2+3+3+7. Some Ruth-Aaron pairs only have one of each factor, so they qualify under either method. The original kind were discovered for 714 Ruth's career record, and 715, the number on the day Aaron passed his record (he went on to get more).
125 is a palindrome in base 4(1331) and in base 20, with the cool name of the vigesimal (from the Latin 'vicesimus', the French 'vingt' is still used for naming some number between 70 and 99) system (65). 20 is also a score, so if someone asks the day of the year, it's six score and five.
The 126th Day of the Year
nine points around a circle form the vertices of \( \binom{9}{4} = 126 \) unique quadrilaterals. That also means that if you draw all the diagonals of the nonagon, you would be using the same 126 sets of four vertices to get 126 intersections.
as 126 = 125 + 1 it is almost obvious that it is the sum of two cubes. It is also the sum of a cube and a square, and it is the first of four consecutive numbers that are the sum of a cube and a square.
In non-leap years, there are 126 days in which the day of the month is prime.
The prime gap that covers the first century with no primes (from 1671800 to 1671899) has length 126 (from 1671781 to 1671907).
The sum of the unique prime factors of 126 is equal to the product of its digits, there is no smaller multi-digit number for which this is true. *Prime Curios
There are 9 choose 5, or 126 ways for a random selection to pick the five spaces on a tic tac toe board for the "first player" in a random game. 36 of these configurations are a "win" for both players. They have both three x's and three O's in a line, since they don't have an order of play. Over 58% of those games are a win for the "first player". Geometrically, a student could think of each random game as a pentagon selected from nine points spaced around a circle.
126 is a palindrome in base 5 (1001) and in base 20(66), six score and six.
The "magic numbers" in Physics are the numbers of nucleons (protons are neutrons) which exactly fill the shells, and thus form very stable isotopes. The numbers are 2, 8, 20, 28, 50 82 and 126. The first six numbers correspond to the elements, helium, oxygen, calcium, nickel, tin, lead, and the element for 126 has not, at this writing, been discovered.
125 and 126 are a Ruth Aaron pair of the second kind. In the first kind prime factors are only counted once, in the second kind they are counted as often as they appear, so 5+5+5 = 2+3+3+7, The original kind were discovered for 714 Ruth's career record, and 715, the number on the day Aaron passed his record (he went on to get more).
On the 126th day of the year 1937, the Hindenburg Zeppelin crashed in New Jersey, (See Day 129)
nine points around a circle form the vertices of \( \binom{9}{4} = 126 \) unique quadrilaterals. That also means that if you draw all the diagonals of the nonagon, you would be using the same 126 sets of four vertices to get 126 intersections.
as 126 = 125 + 1 it is almost obvious that it is the sum of two cubes. It is also the sum of a cube and a square, and it is the first of four consecutive numbers that are the sum of a cube and a square.
In non-leap years, there are 126 days in which the day of the month is prime.
The prime gap that covers the first century with no primes (from 1671800 to 1671899) has length 126 (from 1671781 to 1671907).
The sum of the unique prime factors of 126 is equal to the product of its digits, there is no smaller multi-digit number for which this is true. *Prime Curios
There are 9 choose 5, or 126 ways for a random selection to pick the five spaces on a tic tac toe board for the "first player" in a random game. 36 of these configurations are a "win" for both players. They have both three x's and three O's in a line, since they don't have an order of play. Over 58% of those games are a win for the "first player". Geometrically, a student could think of each random game as a pentagon selected from nine points spaced around a circle.
126 is a palindrome in base 5 (1001) and in base 20(66), six score and six.
The "magic numbers" in Physics are the numbers of nucleons (protons are neutrons) which exactly fill the shells, and thus form very stable isotopes. The numbers are 2, 8, 20, 28, 50 82 and 126. The first six numbers correspond to the elements, helium, oxygen, calcium, nickel, tin, lead, and the element for 126 has not, at this writing, been discovered.
125 and 126 are a Ruth Aaron pair of the second kind. In the first kind prime factors are only counted once, in the second kind they are counted as often as they appear, so 5+5+5 = 2+3+3+7, The original kind were discovered for 714 Ruth's career record, and 715, the number on the day Aaron passed his record (he went on to get more).
On the 126th day of the year 1937, the Hindenburg Zeppelin crashed in New Jersey, (See Day 129)
The 127th Day of the Year
127 is the last prime year day that will be a repdigit in base 2 (1111111)
126 was the sum of two cubes, 127 is the concatenation of two cubes, 1, 27.
The fourth perfect number, 8128, is 127 * 64 , which relates to :
127 is the fourth Mersienne Prime, 27-1. Édouard Lucas verified 2127-1 as prime in 1876, and it remained the largest known prime for over 70 years. He is said to have spent 19 years in checking this 39 digit prime by hand. This remains the largest prime number discovered without the aid of a computer. (Lucas also invented the Towers of Hanoi Puzzle, and the game of dots and boxes which he called "La Pipopipette".)
20 + 21 + 22 + 23 + 24 + 25 + 26 = 127.
French Mathematician Alphones de Polignac is know for two conjectures about prime numbers; the first was that any odd number greater than two could be formed by sum of a power of two and a prime. He was wrong. His statement is now known to be false, as 127 can not be so formed. Although false, his conjecture may be true for all composite numbers. Every exception I have found, like 127 and 149 and 251, are primes.
His other conjecture is related to the idea of twin primes. He conjectured that for every even number, there are an infinite number of primes that distance apart. So far this one is still unproven.
 |
| *Cartoonspot.net |
127 is the sum of the first nine odd primes, 3+ 5+ 7 +.... + 29 = 127
The last three digits of the 11th Mersenne Prime, \( 2^{89}-1 = 162259276829213363391578010288127\) .... ends in 127 , the Mersenne Prime, ends in 127. The next Mersenne Prime is M(127). *Prime Curios.
127 is a palindrome in base 2 of course, all ones, but also in base 9 (121)
127 primes fall between 2000 and 3000. *Prime Curios
127 = 1! + 3! + 5!
If you find all the prime pairs that add up to 1000, there are 127 of them. *Prime Curios
127 mm = 5 inches. Handy reference.
127 can be expressed as the sum of factorials of the first three odd numbers (1! + 3! + 5!). And in a rare equivalence, 127 cm is equal to 50 inches. HT Don S. McDonald @McDONewt
127 is the smallest odd prime that can't be written as a prime P + 2^x for some integer.
127 x \(\sqrt{62}\) is almost an integer, 999.998999999...
The Prime Gap of 14 days between 109 and 127 is the Longest Prime Gap in the year Days. There will be three such gaps this year, but the next is about four months away, so lots of prime days in your near future.
The Prime Gap of 14 days between 109 and 127 is the Longest Prime Gap in the year Days. There will be three such gaps this year, but the next is about four months away, so lots of prime days in your near future.
The 128th Day of the Year
128 is The largest known even number that can be expressed as the sum of two primes in exactly three ways. (Find them) *Prime Curios How many smaller numbers (and which) are there that can be so expressed?
But, it can not be expressed as the sum of distinct squares, for any number of squares.
And it is the largest such number, ever.... no, I mean EVER. The very last.
128 = 2^8, so in binary it is a 1 followed by 7 zeros, which makes it also 4^4, and in base 4 its a 2 with three zeros. But it's also 8^2, so in base eight its a 2 with two zeros,
128 is The largest known even number that can be expressed as the sum of two primes in exactly three ways. (Find them) *Prime Curios How many smaller numbers (and which) are there that can be so expressed?
But, it can not be expressed as the sum of distinct squares, for any number of squares.
And it is the largest such number, ever.... no, I mean EVER. The very last.
128 = 2^8, so in binary it is a 1 followed by 7 zeros, which makes it also 4^4, and in base 4 its a 2 with three zeros. But it's also 8^2, so in base eight its a 2 with two zeros,
128 is a power of two, and all of its digits are powers of two. I don't know of any other.
128 is also the largest number that cannot be expressed as the sum of distinct squares. *Number Gossip. (Surprisingly, there are only 31 numbers that can not be expressed as the sum of distinct squares. )
128 can be expressed by a combination of its digits with mathematical operators thus 128 = 28 - 1, making it a Friedman number in base 10 (Friedman numbers are named after Erich Friedman, as of 2013 an Associate Professor of Mathematics and ex-chairman of the Mathematics and Computer Science Department at Stetson University, located in DeLand, Florida.)
128 the sum of the factorials of the first three prime numbers, 2! + 3! + 5! =128.
Some nice relationships between 128 and its digits, 128 + (1+2+8) = 139, a prime number. But 128 + (8 + 1) is 137, also prime, and 128 + (2 + 1) is 131, a prime, AND 128 +( 8+2 ) is not prime, but 138 is between a twin prime pair. ..... And 1*2*8 = 16 is a divisor of 128.
And that pair of cousin primes, 127 and 131, are the largest such pair with a power of two (128) between them.
The name for a particular 7th dimensional Hyperplex with 128 vertices is a Hepteract. Dazzle your friends.
Oh, I told you 128 is the 7th power of two.... but there are no more three digit numbers that are 7th powers...
And if you like to keep score, 128 is 6 score and 8. In old commercial terminology, a schock was a lot of 60 items, so 128 is also two shock and 8, or 28 in sexigesimal (base sixty). The number of stalks of corrn or wheat (supposedly) gathered and stood on ends in the fields to dry, like in "When the frost is on the Pumpkin and the Fodders in the shock. "
128 is divisible by four so it is the difference of two squares of numbers that differ by 2, and since 128 / 4 = 32, the numbers must straddle 31, 33² - 31² = 128.
But it is also divisible by eight, so it is the difference of two squares of numbers that differ by four(there is a power of two relation working here, which students might find). And since 128/8 = 16, 18² - 14² = 128
And in 1968 the 128 K Mac was the hottest desktop computer around.
The 129th Day of the Year
129 is the smallest number with four representations as a sum of three positive (but not necessarily distinct) squares: 129 = 12 + 82 + 82 = 22 + 22 + 112 = 22 + 52 + 102 = 42 + 72 + 82 .
129 is also the sum of the first ten primes.
129 is the fourth number in a row that is the sum of a square and a cube, and 129 that may be accomplished in two different ways.
And in 1968 the 128 K Mac was the hottest desktop computer around.
The 129th Day of the Year
129 is the smallest number with four representations as a sum of three positive (but not necessarily distinct) squares: 129 = 12 + 82 + 82 = 22 + 22 + 112 = 22 + 52 + 102 = 42 + 72 + 82 .
129 is also the sum of the first ten primes.
129 is the fourth number in a row that is the sum of a square and a cube, and 129 that may be accomplished in two different ways.
129 is the smallest sum of distinct seventh powers (17 + 27).
It's also \( 2^7 + 2^0 \) and thus a palindrome in base two, (10000001) and a repdigit palindrome in base 6(333).
If you concatenate the prime divisors of 129, 3 and 43, you get 343, you get a prime to a prime power, \( 7^3\)
129 is a Happy Number, if you sum the square of the digits, and continue iterating that process on each new number, you end up at one. Unhappily, the origin of the name and the creator are unknown. It was popularized by Leeds Math Professor Reg Allenby, who heard about it from his daughter who picked it up at school. Suspected origin is Russia according to the late Richard Guy.
And if you've not spent some time in Western Ky, and perhaps even if you have, you might not guess where the official Banana Capital of the US is. It's in the little town of Fulton, Ky, along the train route from New Orleans to Chicago, and Fulton had the distinction of being the place where Union Fruit company chose to pause the trains bringing fresh bananas along the way to re-ice them for the rest of their journey.At one time over 70% of Bananas shipped into the US came through Fulton. About 13 miles away is the even smaller town of Wingo, formerly called Wingo Station ( because it set along the same New Orleans and Ohio rail line passing through Fulton. And what they have in common other than that, is the reason I mention them today, they are on the ends of Ky Route 129. They are just a pretty spring drive of 40 miles from here in Possum Trot.
"Oh, the humanity, and all the passengers screaming around here!" Herbert Morrison broadcasting live over WLS Chicago from NAS Lakehurst New Jersey as he reported on the burning of the Hydrogen filled Zeppelin, The Hindenburg, on May 6, 1937 (that was the 126th day of that year), but it's number was LZ129..
 |
| *Wikipedia |
The 130th Day of the Year
130 is the sum of the factorials of the first five terms of the Fibonacci sequence.
130 is the sum of the squares of its four smallest divisors, ( \( 1^2 + 2^2 + 5^2 + 10^2 = 130 \)
130 is also the only number equal to the sum of the squares of its first 4 divisors: 130 = 1^2 + 2^2 + 5^2 + 10^2.*Prime Curios
This is the 46th day of the year that is the sum of two squares, 3^2 + 11^2.
130 is the sum of consecutive odd powers of 5, 5^1 + 5^3
Haven't mentioned the hexgonal numbers much this year so far, but 130 is the largest number that cannot be written as the sum of four hexagonal numbers.
Hexagonal numbers are given by the formula H(n) = n(2n-1), and produce the sequence 1, 6, 15, 28, 45, 66, 91... (can you find numbers that ARE the sum of four ) (All the even perfect numbers are in that sequence..)
 |
| *Wikipedia |
The 131st Day of the Year
131 is the sum of three two-digit primes (31 + 41 + 59) whose concatenation is the decimal expansion of pi (3.14159...).
Any ordering of the digits of 131 is still prime. This is called an "absolute" prime and a permutable prime.
131 is the sum of three prime numbers that all begin with the same digit. *Prime Curios
bonus: 131 is the 32nd prime and the sum of the digits of both numbers is 5.
32 & 131 is the smallest n, P(n) pair with this property. Such numbers are often called Honaker Primes after G. L. Honaker, Jr, . There is only one more such prime that is a year day.
Since 2 (131)+ 1 = 263 is also prime, 131 is called a Sophie Gerrmain prime. Sometimes the prime created by the 2p+1 process is also a Sophie Germain Prime, for example 11 is SGP since 2x11+1 = 23 is prime, and 23 is a SGP since 223+1 = 47 is also prime.
The reciprocal of 131 repeats with a period of 130 digits, 1/131 =0.007633587786259 54198473282442748091603053435114503816793893129770992366412213740458 015267175572519083969465648854961832...
131 is the smallest integer for which the sum of its digits in every base B = 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 is prime . \(10000011_2, 11212_3, 2003_4\) and the digit sums are 3, 7, and 5... all primes.
The 131st Fibonacci (1066340417491710595814572169) is the smallest Fibonacci prime which contains all the digits from 0 to 9. *Prime Curios
US 131 is a road mostly through Michigan ending at the beautiful town of Petoskey, on the shores of Lake Michigan. Important as the birthplace of Claude Shannon, the father of information theory.
Think like Fibonacci, 131 = 0! + 1! + 1! + 2! + 3! +5!
The reciprocal of 131 repeats with a period of 130 digits, 1/131 =0.007633587786259 54198473282442748091603053435114503816793893129770992366412213740458 015267175572519083969465648854961832...
131 is the smallest integer for which the sum of its digits in every base B = 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 is prime . \(10000011_2, 11212_3, 2003_4\) and the digit sums are 3, 7, and 5... all primes.
The 131st Fibonacci (1066340417491710595814572169) is the smallest Fibonacci prime which contains all the digits from 0 to 9. *Prime Curios
US 131 is a road mostly through Michigan ending at the beautiful town of Petoskey, on the shores of Lake Michigan. Important as the birthplace of Claude Shannon, the father of information theory.
Think like Fibonacci, 131 = 0! + 1! + 1! + 2! + 3! +5!
One fact about 131 reminds me of some early number theorems, Find a number that divided by four has a remainder of three, and divided by 3 has a remainder of 2, and divided by 2 has a remainder of 1....
131 is a knockout prime, since you can "knockout' any digit and leave a prime, 31, 11, 13. Chris Maslanka created the term. on a twitter feed with me. The symbol for a number like 131 where the three digits form a prime number is KP(3,3), a three digit prime; and with any one crossed out, they still form a prime, so it's KP(3,2) and if all three of the digits were prime, it would be KP(3,1) but we no longer accept one as prime. I used KP for knockout Prime over another good suggestion. It is also a Permutable prime for which PP(3,3) is an appropriate symbol. For the story of my "discovery" see Knockout Primes, and a New Notation.
132 and its reversal (231) are both divisible by the prime 11 (132/11 = 12, 231/11 = 21). Note that the resulting quotients are also reversals. *Prime Curios
132 is the last year day which will be a Catalan Number. The Catalan sequence was described in the 18th century by Leonhard Euler, who was interested in the number of different ways of
dividing a polygon into triangles (the octagon can be divided into 6 triangles 142 ways. The sequence is named after Eugène Charles Catalan, who discovered the connection to parenthesized expressions during his exploration of the Towers of Hanoi puzzle.
132 is the smallest number with this property,
132 and its reversal (231) are both divisible by the prime 11 (132/11 = 12, 231/11 = 21). Note that the resulting quotients are also reversals. *Prime Curios
132 is the last year day which will be a Catalan Number. The Catalan sequence was described in the 18th century by Leonhard Euler, who was interested in the number of different ways of dividing a polygon into triangles (the octagon can be divided into 6 triangles 142 ways. The sequence is named after Eugène Charles Catalan, who discovered the connection to parenthesized expressions during his exploration of the Towers of Hanoi puzzle.
If you take the sum of all 2-digit numbers you can make from 132, you get 132: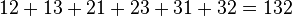 . 132 is the smallest number with this property. The other two are both multiples of 132.
. 132 is the smallest number with this property. The other two are both multiples of 132.
If you take the sum of all 2-digit numbers you can make from 132, you get 132:
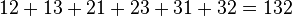 . 132 is the smallest number with this property. The other two are both multiples of 132.
. 132 is the smallest number with this property. The other two are both multiples of 132. Students, it should be obvious that all permutations of 1,2,3 will produce the same result. But can you see what 015, 033, 141, 222 will also go to the same absorbing state. Use a similar analysis to find numbers that end in 264.
132 = 2 * 3 * 11, these three factors can be arranged in three orders to produce a prime, 2311, 2113, and 1123. (and of course, no arrangement of the original three digits can form a prime ) and of all the 12 permutations of the digits of the three factors, there are 7; (1123, 1213, 1321, 2113, 2131, 2311, and 3121) that are all prime.
And speaking of the factors 11, 2, 3, a nice palindromic expression for 132 is 11*2*3+3*2*11
132 is a Harshad (Joy-Giver) number, since it is divisible by the sum of its digits.
132 = 2 * 3 * 11, these three factors can be arranged in three orders to produce a prime, 2311, 2113, and 1123. (and of course, no arrangement of the original three digits can form a prime ) and of all the 12 permutations of the digits of the three factors, there are 7; (1123, 1213, 1321, 2113, 2131, 2311, and 3121) that are all prime.
And speaking of the factors 11, 2, 3, a nice palindromic expression for 132 is 11*2*3+3*2*11
132 is a Harshad (Joy-Giver) number, since it is divisible by the sum of its digits.
It is also called a refactorable number because it is divisible by the number of its divisors, 12.
132 is also a self number, as there is no number n which added to the sum of the digits of n is equal to 132.
132 is not a palindrome in any base 2-12, but in base 7(246) it has digits that are each the double of the digits in 132. (I just noticed that, and wonder how often something like that happens?)
The 133rd Day of the Year
133 is a "happy number". If you sum the squares of the digits and then repeat the process and the sum will eventually come to one. (12 + 32+32= 19 ... === 82 === 68 === 100 ====1) Some numbers, "unhappy ones", never reach one. (Student's might explore happy numbers to find how many times the process must be iterated for different numbers to reach one, for example I (33) = 5 Alternatively, curious students may wonder what happens to the "unhappy" numbers if they never reach one.)
133 is also a Harshad (Joy-Giver) number, since it is divisible by the sum of its digits.
133 is a repdigit in base 11 (111) and base 18 (77),
133 is the sum of the squares of the first three semi-primes, and is a semi-prime itself. it is the smallest number with this property.
According to one classification, there are 133 species of mammal on the Earth, and 1/7th of them are Bats. *Number Freak, Derrick Niederman
133= 42 + 62 +92
And Jim Wilder @wilderlab posted this interesting observation about 133 and it's reversal, 331.
133, and 134 were used by Euler in generating birectangular Heronian tetrahedra. He created a method for deriving them from equal sums of fourth powers \$ p^4 + q^4 = r^4 + s^4\$ and used 133 and 134 on one side, and 59 and 158 on the other. The actual side lengths of the three perpendicular edges created from this quartet were over 332,000,000.
133 is the smallest integer, n, for which 10 n +(1or 3 or 7 or 9) are all composite. Prime Curios
The Dewey Decimal system classification for numerology is 133.533, and if you add the first to the reverse of the second 133+335=666....
The 134th Day of the Year
133, and 134 were used by Euler in generating birectangular Heronian tetrahedra. He created a method for deriving them from equal sums of fourth powers \( p^4 + q^4 = r^4 + s^4\) and used 133 and 134 on one side, and 59 and 158 on the other. The actual side lengths of the three perpendicular edges created from this quartet were over 332,000,000.
134 has only two prime factors (67 and 2){called a bi-prime or a semiprime, it is the 45th semiprime of the year to date.} . Note that 1342 - 672 = 13467, which is the base numbers concatenated. *Prime Curios
134 is the sum of 8C1 + 8C3 + 8C4
134 is the 19th day of the year that is the sum of three positive cubes.
And 134 is t he maximal number of regions the plane can be divided with 12 circles.
It is not possible to append a single digit to 134 and produce a prime. >
In this politically charged atmosphere, individuals in the military might want to be aware that, the American UCMJ;is the catch-all article, for offences "not specifically mentioned in this chapter." Used to prosecute a wide variety of offences, from cohabitation by personnel not married to each other to statements critical of the U.S. President. Some prisoners, including Abu Ghraib were tagged with this number. Wik
The 135th Day of the year.
135 is the smallest non-trivial SP (sum times product) number. If you take the sum of the digits of a number, and also the product of the digits, and then multiply the two outcomes, there are only three positive numbers for which you will get the original value. One works, trivially. The other two are 135 and 144. 135-> (1+3+5)*(1*3*5) = 9*15=135. 144->(1+4+4)*(1*4*4)= 9 * 16 = 144.
A Good exercise for students is to take the SP product in a iteration to find out if it goes to zero, or repeats some pattern, or lands eventually on one of these three fixed points. (Try it with your students). 23->5*6 = 30. 30-> 3*0 = 0.... fixed point.
132 is also a self number, as there is no number n which added to the sum of the digits of n is equal to 132.
132 is not a palindrome in any base 2-12, but in base 7(246) it has digits that are each the double of the digits in 132. (I just noticed that, and wonder how often something like that happens?)
The 133rd Day of the Year
133 is a "happy number". If you sum the squares of the digits and then repeat the process and the sum will eventually come to one. (12 + 32+32= 19 ... === 82 === 68 === 100 ====1) Some numbers, "unhappy ones", never reach one. (Student's might explore happy numbers to find how many times the process must be iterated for different numbers to reach one, for example I (33) = 5 Alternatively, curious students may wonder what happens to the "unhappy" numbers if they never reach one.)
133 is also a Harshad (Joy-Giver) number, since it is divisible by the sum of its digits.
133 is a repdigit in base 11 (111) and base 18 (77),
133 is the sum of the squares of the first three semi-primes, and is a semi-prime itself. it is the smallest number with this property.
According to one classification, there are 133 species of mammal on the Earth, and 1/7th of them are Bats. *Number Freak, Derrick Niederman
133= 42 + 62 +92
And Jim Wilder @wilderlab posted this interesting observation about 133 and it's reversal, 331.
133, and 134 were used by Euler in generating birectangular Heronian tetrahedra. He created a method for deriving them from equal sums of fourth powers \$ p^4 + q^4 = r^4 + s^4\$ and used 133 and 134 on one side, and 59 and 158 on the other. The actual side lengths of the three perpendicular edges created from this quartet were over 332,000,000.
133 is the smallest integer, n, for which 10 n +(1or 3 or 7 or 9) are all composite. Prime Curios
The Dewey Decimal system classification for numerology is 133.533, and if you add the first to the reverse of the second 133+335=666....
The 134th Day of the Year
133, and 134 were used by Euler in generating birectangular Heronian tetrahedra. He created a method for deriving them from equal sums of fourth powers \( p^4 + q^4 = r^4 + s^4\) and used 133 and 134 on one side, and 59 and 158 on the other. The actual side lengths of the three perpendicular edges created from this quartet were over 332,000,000.
134 has only two prime factors (67 and 2){called a bi-prime or a semiprime, it is the 45th semiprime of the year to date.} . Note that 1342 - 672 = 13467, which is the base numbers concatenated. *Prime Curios
134 is the sum of 8C1 + 8C3 + 8C4
134 is the 19th day of the year that is the sum of three positive cubes.
And 134 is t he maximal number of regions the plane can be divided with 12 circles.
It is not possible to append a single digit to 134 and produce a prime. >
In this politically charged atmosphere, individuals in the military might want to be aware that, the American UCMJ;is the catch-all article, for offences "not specifically mentioned in this chapter." Used to prosecute a wide variety of offences, from cohabitation by personnel not married to each other to statements critical of the U.S. President. Some prisoners, including Abu Ghraib were tagged with this number. Wik
The 135th Day of the year.
135 is the smallest non-trivial SP (sum times product) number. If you take the sum of the digits of a number, and also the product of the digits, and then multiply the two outcomes, there are only three positive numbers for which you will get the original value. One works, trivially. The other two are 135 and 144. 135-> (1+3+5)*(1*3*5) = 9*15=135. 144->(1+4+4)*(1*4*4)= 9 * 16 = 144.
A Good exercise for students is to take the SP product in a iteration to find out if it goes to zero, or repeats some pattern, or lands eventually on one of these three fixed points. (Try it with your students). 23->5*6 = 30. 30-> 3*0 = 0.... fixed point.
\(135 \equiv 3 (\mod 6)\) and so 135 is expressible as the difference of two squares, using bases three apart. The two bases must sum to 135 / 3 = 45. So 21 and 24 should work, and 24² - 21² = 135
135 = 3^3 * 5, with only two distinct factors, 3 and 5. If you start with three, and square 5 consecutive integers, \(3^2 + 4^2 + 5^2 + 6^2 + 7^2 = 135\) *Prime Curios
135 = 11 + 32 + 53. *What's So Special About This Number (can you find others?) There are only two year dates that have this property. The second is larger and may take you forty days and nights to find.
135 is the "partition number", or the number of ways to partition 14. We still do not know if there are an infinite number of "partition numbers" which are divisible by 3, although we do know there are an infinite number divisible by 2
\( 135 = 11 x^2 + 11x +3\) is a simple quadratic that was an important element in Apery's proof that is irrational. To four decimal digits accuracy, it is 1.2020.... the year I'm writing this.
Quick! How many primes from 1000 to 2000? 135, of course!
135 = 3^3 * 5, with only two distinct factors, 3 and 5. If you start with three, and square 5 consecutive integers, \(3^2 + 4^2 + 5^2 + 6^2 + 7^2 = 135\) *Prime Curios
135 = 11 + 32 + 53. *What's So Special About This Number (can you find others?) There are only two year dates that have this property. The second is larger and may take you forty days and nights to find.
135 is the "partition number", or the number of ways to partition 14. We still do not know if there are an infinite number of "partition numbers" which are divisible by 3, although we do know there are an infinite number divisible by 2
\( 135 = 11 x^2 + 11x +3\) is a simple quadratic that was an important element in Apery's proof that is irrational. To four decimal digits accuracy, it is 1.2020.... the year I'm writing this.
Quick! How many primes from 1000 to 2000? 135, of course!
The interior angles of a regular Octagon are \(135^o\)
This day in Roman numerals is not suitable for minors, CXXXV.
135 is a palindrome in base 6( 343) , and base 7(252)
Two planets that are \( 135^o \) apart are called sesquiquadrate, and it is said they are in astrological aspect. The aspect terms seems to have been created by Johannes Kepler. And for students, the other big long word means one and one half quadrants. I'll give you another of those sesquipedalian words down the way a bit.
135 = 1^1 + 3^2 + 5^3. The only other examples I know of are 175, 518, and 598.
The function \( (11 x 10^k + 19)/3 \) generates some unusual primes. If you plug in 135, you get a number beginning with two followed by 135-2 sixes and ending in 73. For example with k=4 you get 36673. Not sure what leads to functions like this, but I have come across several of them over the years.
And if you need to get out of Indianapolis and run down to the Blue Grass, Indiana State Road 135 runs to the boarder on the Ohio at Mauckport, just west of Louisville. Pretty (mostly) two lane roads with lots of little towns and pretty farms.
The 136th Day of the Year
136 is "power friendly" with 244. \(244 =1 ^3 + 3^3 + 6^3\) and \(136 = 2^3 + 4^3 + 4^3\)
(Only one other number pair share this relation. Can you find them?)
The sum of all prime factors of 136 is equal to the reversal of \$ \pi(136)\$. \$ \pi(n)\$ is the number of primes less than n (so \(\pi(136)=32 \) and the sum of the prime factors of 136 is 2+2+2+17 =23, the revrsal of 32.
136 is the number of walks of length 9 between two adjacent vertices in the cycle graph C_8 (A,B,C,D,E,F,G,H)
136 is a factor of \( N_Edd\) , the Eddington number, calculated by Arthur Eddington in 1938 for the number of protons in the observable universe. The number can be factored into 136 (2^156) which is about 2^80.
136 is the sum of the first 16 numbers, the numbers in a four by four magic square. It is the magic square associated with the planet Jupiter, and appears in the Albrecht Durer woodcut, "Melancholia I,"
on the wall behind the suffering "thinker." Some suggest it was there to represent the association of Jupitar (Jovia) and joviality to balance the mood of the work.136 is the number of walks of length 9 between two adjacent vertices in the cycle graph C_8 (A,B,C,D,E,F,G,H)
136 is a factor of \( N_Edd\) , the Eddington number, calculated by Arthur Eddington in 1938 for the number of protons in the observable universe. The number can be factored into 136 (2^156) which is about 2^80.
136 is the sum of the first 16 numbers, the numbers in a four by four magic square. It is the magic square associated with the planet Jupiter, and appears in the Albrecht Durer woodcut, "Melancholia I,"
Lots of numbers are expressible as the sum of two squares, but 136 is the smallest that can be expressed where neither of the two are squares of a prime. *Prime Curios
136 is a triangular number, which means it's the sum of consecutive integers from 1 to n, Find n. (hint: get rid of the prime digit.)
In binary 136 is written as the concatenation of two binary "Eights". (10001000). In base 9 is a palindrome (161) and in Hexdecimal it is a repdigit (88).
The 137th Day of the Year
137 is the sum of the squares of the first seven digits of pi, 32+ 12 + 42 + 12 + 52 + 92 + 22 = 137. *Prime Curios (There is no smaller number of digits of pi for which this is true.) If you add the square of the next digit (6^2) you get another prime which is a permutation of the digits of this one, 173.
137 is the third term in a sequence of primes that can be created by staring with 7 and creating a new term by adding a single digit to the front of the previous term; 7, 37, 137 ... It is possible to create a sequence of 15 Prime numbers in this way. OEIS
Like palindromes, Don McDonald reminded me that 10/137 is a nice one, the period eight repeating palindrome .07299270...
If you just use 1/137 you get 0.00729927.... which was also thought to be the fine structure constant in physics according to Eddington.It turned out he was very close, but not quite exact. What if you tried 100/137?
Wolfgang Pauli died in hospital room 137, after a lifetime trying to prove that 137 was the fine structure constant. It's close, but not so.
137 is the largest prime factor of 123456787654321*Prime Curios
137 is the 33rd Prime number and is a twin prime with 139, it's a Pythagorean prime, 11^2 + 4^2, and it is a KnockoutPrime (3,2) it remains prime if you knock out any one character leaving two.
137 is not a palindrome in any base between 2 and 135.... Called a strictly non-palindrome.
137 is the first of twelve consecutive primes with equal gaps around the center, sort of a palindrome of gaps to make up for being a non-palindrome. The 11 gaps between them is 2, 10, 2, 6, 6, 4, 6, 6, 2, 10, 2, ending in 191.
137 divides 11111111, and all the other eight digit repdigits.
And direct from Prime Curios, and coffee loving mathematicians everywhere, The full chemical name for caffeine is 1,3,7-trimethylxanthine.
The 138th Day of the Year:
138 is a sphenic number(the product of three primes from the Greek for "wedge shaped") and is the smallest product of 3 primes, such that in base 10, the third prime is a concatenation of the other two: (2)(3)(23)
138 is the sum of four consecutive primes (29 + 31 + 37 + 41),
and 138 can be written in palindromic expression, 138 = 19+2*7*2+91 *@AmbrigrammDesign.
138 is an Ulam Number, a member of the sequence created by a sieve process by Stan Ulam in 1964. It begins with the numbers 1, 2, and then each successive term is the smallest larger number that is the sum of two distinct numbers in the sequence, in a single way. The first few numbers are 1, 2, 3, 4, 6, 8, 11,,, Five is missing because its sum can be created in two different ways, 2+3 or 1+4.
The 139th day of the year; 139 and 149 are the first consecutive primes differing by 10. *David Wells, Curious and Interesting Numbers.
139 = 3x3+11x11+3x3 *@AmbigrammDesign
The 140th Day of the Year;
140 is the sum of the squares of the first seven positive integers. 12 + 22 + 32 + 42 + 52 + 62 + 72 = 140. *Prime Curios (and 7 is the largest prime factor of 140 And the 7 consecutive numbers starting with 140, all have an even number of prime factors, 140 is 2x2x5x7.
140 is the magic constant of this 5x5 square by *Srinivasa Raghave K Can you see how to easily make one for day 135, or 145? Jeff Miller's Web site on the Earliest Use of Math Words says that Frenicle de Bessy used the term magic in the title to his book, Des quarrez ou tables magiques, published posthumously in 1693, twenty years after his death. The first use in English was the same year in "A New Historical Relation of the Kingdom of Siam." Appropriate to have de Bessey mentioned here, as he first noted the cubic relation of the Taxi-cab number, 1729 and Srinivasa is a big fan, I believe, of Ramanujan.
Bus 142 (the "Magic Bus"), whose number is clearly visible on the bus that Christopher McCandless lived in until his death in Alaska, features prominently on the bus in the film made about his life called Into the Wild
The 143rd Day of the Year
there are 143 three-digit primes.
Also, 143^2 is a divisor of 143143.HT to Matt McIrvin who found the pattern for numbers such that n^2 divides n.n (where the dot represents concatenation) and then found it is at OEIS I should point out that every number greater than one for which this is true involves the digits 143, in order, and includes a mystery offering from one-seventh.
143 is also the number of moves that it takes 11 frogs to swap places with 11 toads on a strip of 2(11) + 1 squares (or positions, or lily pads) where a move is a single slide or jump. This activity dates back to the 19th century, and the incredible recreational mathematician, Edouard Lucas *OEIS.
Prof. Singmasters Chronology of Recreational Mathematics suggests that this was first introduced in the American Agriculturalist in 1867, and I have an image of the puzzle below. The fact that they call it, "Spanish Game" suggests it has an older antecedent. (anyone know more?)
143 is the smallest composite number, n, such that 5^n + 2 is prime. (That's some big number) *Prime Curios
143 is the sum of seven consecutive primes, beginning with 11.
There is no decimal number n, such that n + (sum of its digits) = 143.
Waring's problem tells us that every number is the sum of at most 143 seventh powers.
\( 3^2 + 4^2 = 5^2 \) AND
\( 3^3+4^3+5^3=6^3 \)
BUT
\(3^4+4^4 + 5^4+6^4=7^4-143\) Another beautiful pattern, spoiled by an ugly truth!
143 is a repdigit in base 12 (BB) (that's eleven twelves plus eleven)
The 144th Day of the year.
144 is the largest possible SP (sum times product) number. If you take the sum of the digits of a number, and also the product of the digits, and then multiply the two outcomes, there are only three positive numbers for which you will get the original value. One works, trivially. The other two are 135 and 144. 135-> (1+3+5)*(1*3*5) = 9*15=135. 144->(1+4+4)*(1*4*4)= 9 * 16 = 144.
.A Good exercise for students is to take the SP product in a iteration to find out if it goes to zero, or repeats some pattern, or lands eventually on one of these three fixed points(that's four fixed points if you count zero). (Try it with your students). 23->5*6 = 30. 30-> 3*0 = 0.... fixed point.
144 is the only non-trivial square in the Fibonacci Sequence.In fact, there are only four Fibonacci numbers that are perfect powers, 0, 1, 8, and 144. And we haven't known that for so very long. Here is the story from , Professor Stewart's Incredible Numbers
In 1913 R. D. Carmichael proved his conjecture that for any Fibonacci Number F(n), greater than F(12)=144, has at least one prime factor that is not a factor of any earlier Fibonacci number.
\(144^5 = 27^5 + 84^5 + 110^5 + 133^5 \) This counter-example disproved Euler's Conjecture that n nth powers are needed to sum to an nth power. It is also part of one of the shortest papers ever published in a math journal(two sentences)
(Squares are important in knowing if a number, n is Fibonacci or not. N is Fibonacci IFF one or both of \(5n^2 \pm 4\) is a perfect square. )
144 is also the smallest square number which is also a square when its digits are reversed 144 = 12 2 while 441= 212
144 is the second smallest even square which has no prime for its two adjacent numbers, 143 = 11 x 13, 145 = 5 x 29 . There is only one more year after this which is a square with no adjacent prime.
136 is a triangular number, which means it's the sum of consecutive integers from 1 to n, Find n. (hint: get rid of the prime digit.)
In binary 136 is written as the concatenation of two binary "Eights". (10001000). In base 9 is a palindrome (161) and in Hexdecimal it is a repdigit (88).
The 137th Day of the Year
137 is the sum of the squares of the first seven digits of pi, 32+ 12 + 42 + 12 + 52 + 92 + 22 = 137. *Prime Curios (There is no smaller number of digits of pi for which this is true.) If you add the square of the next digit (6^2) you get another prime which is a permutation of the digits of this one, 173.
137 is the third term in a sequence of primes that can be created by staring with 7 and creating a new term by adding a single digit to the front of the previous term; 7, 37, 137 ... It is possible to create a sequence of 15 Prime numbers in this way. OEIS
Like palindromes, Don McDonald reminded me that 10/137 is a nice one, the period eight repeating palindrome .07299270...
If you just use 1/137 you get 0.00729927.... which was also thought to be the fine structure constant in physics according to Eddington.It turned out he was very close, but not quite exact. What if you tried 100/137?
Wolfgang Pauli died in hospital room 137, after a lifetime trying to prove that 137 was the fine structure constant. It's close, but not so.
137 is the largest prime factor of 123456787654321*Prime Curios
137 is the 33rd Prime number and is a twin prime with 139, it's a Pythagorean prime, 11^2 + 4^2, and it is a KnockoutPrime (3,2) it remains prime if you knock out any one character leaving two.
137 is not a palindrome in any base between 2 and 135.... Called a strictly non-palindrome.
137 is the first of twelve consecutive primes with equal gaps around the center, sort of a palindrome of gaps to make up for being a non-palindrome. The 11 gaps between them is 2, 10, 2, 6, 6, 4, 6, 6, 2, 10, 2, ending in 191.
137 divides 11111111, and all the other eight digit repdigits.
And direct from Prime Curios, and coffee loving mathematicians everywhere, The full chemical name for caffeine is 1,3,7-trimethylxanthine.
The 138th Day of the Year:
138 is a sphenic number(the product of three primes from the Greek for "wedge shaped") and is the smallest product of 3 primes, such that in base 10, the third prime is a concatenation of the other two: (2)(3)(23)
138 is the sum of four consecutive primes (29 + 31 + 37 + 41),
and 138 can be written in palindromic expression, 138 = 19+2*7*2+91 *@AmbrigrammDesign.
138 is an Ulam Number, a member of the sequence created by a sieve process by Stan Ulam in 1964. It begins with the numbers 1, 2, and then each successive term is the smallest larger number that is the sum of two distinct numbers in the sequence, in a single way. The first few numbers are 1, 2, 3, 4, 6, 8, 11,,, Five is missing because its sum can be created in two different ways, 2+3 or 1+4.
138 is a palindrome in base 8(212)
The 139th Day of the Year:
The 139th Day of the Year:
The 139th day of the year; 139 and 149 are the first consecutive primes differing by 10. *David Wells, Curious and Interesting Numbers.
139 = 9*8+7*6+5*4+3*2-1 *Prime Curios
139 is the sum of five consecutive prime numbers( 19+ 23+ 29 +31+ 37)
139 = 3x3+11x11+3x3 *@AmbigrammDesign
139 is also a Happy number, A happy number is a number defined by the following process: Starting with any positive integer, replace the number by the sum of the squares of its digits, and repeat the process until the number equals 1 (where it will stay),or it loops endlessly in a cycle which does not include 1. Those numbers for which this process ends in 1 are happy numbers, while those that do not end in 1 are unhappy numbers (or sad numbers).For example, 19 is happy, as the associated sequence is:
1^2 + 9^ 2 = 82
8^ 2 + 2^ 2 = 68
6 ^2 + 8^2 = 100 1^ 2 + 0^2 + 0^2 = 1
The happy numbers up to 1,000 are: 1, 7, 10, 13, 19, 23, 28, 31, 32,44, 49, 68, 70, 79, 82, 86, 91, 94, 97, 100, 103, 109, 129, 130, 133, 139, 167,176, 188, 190, 192, 193, 203, 208, 219, 226, 230, 236, 239, 262, 263, 280, 291,293, 301, 302, 310, 313, 319, 320, 326, 329, 331, 338, 356, 362, 365, 367, 368,376, 379, 383, 386, 391, 392, 397, 404, 409, 440, 446, 464, 469, 478, 487, 490,496, 536, 556, 563, 565, 566, 608, 617, 622, 623, 632, 635, 637, 638, 644, 649,653, 655, 656, 665, 671, 673, 680, 683, 694, 700, 709, 716, 736, 739, 748, 761,763, 784, 790, 793, 802, 806, 818, 820, 833, 836, 847, 860, 863, 874, 881, 888,899, 901, 904, 907, 910, 912, 913, 921, 923, 931, 932, 937, 940, 946, 964, 970,973, 989, 998, 1000.
The happiness of a number is unaffected by rearranging the digits, and by inserting or removing any number of zeros anywhere in the number. I propose the use of the term principle Happy numbers for those that do not contain a zero, or an reordering of a previous happy number. That would reduce the above list to the following 31, and makes searches more direct since no descending sequences of digits can exist. 1, 7, 13, 19, 23, 28, 44, 49, 68, 79, 129, 133, 139, 167, 188, 226, 236, 239, 338, 356, 367, 368, 379, 446, 469, 478, 556, 566, 888, 899, 998,(The earliest I have ever found this term was in an article in the Bulletin of the California Mathematics Council in 1970. Does anyone know of an earlier usage?")
1^2 + 9^ 2 = 82
8^ 2 + 2^ 2 = 68
6 ^2 + 8^2 = 100 1^ 2 + 0^2 + 0^2 = 1
The happy numbers up to 1,000 are: 1, 7, 10, 13, 19, 23, 28, 31, 32,44, 49, 68, 70, 79, 82, 86, 91, 94, 97, 100, 103, 109, 129, 130, 133, 139, 167,176, 188, 190, 192, 193, 203, 208, 219, 226, 230, 236, 239, 262, 263, 280, 291,293, 301, 302, 310, 313, 319, 320, 326, 329, 331, 338, 356, 362, 365, 367, 368,376, 379, 383, 386, 391, 392, 397, 404, 409, 440, 446, 464, 469, 478, 487, 490,496, 536, 556, 563, 565, 566, 608, 617, 622, 623, 632, 635, 637, 638, 644, 649,653, 655, 656, 665, 671, 673, 680, 683, 694, 700, 709, 716, 736, 739, 748, 761,763, 784, 790, 793, 802, 806, 818, 820, 833, 836, 847, 860, 863, 874, 881, 888,899, 901, 904, 907, 910, 912, 913, 921, 923, 931, 932, 937, 940, 946, 964, 970,973, 989, 998, 1000.
The happiness of a number is unaffected by rearranging the digits, and by inserting or removing any number of zeros anywhere in the number. I propose the use of the term principle Happy numbers for those that do not contain a zero, or an reordering of a previous happy number. That would reduce the above list to the following 31, and makes searches more direct since no descending sequences of digits can exist. 1, 7, 13, 19, 23, 28, 44, 49, 68, 79, 129, 133, 139, 167, 188, 226, 236, 239, 338, 356, 367, 368, 379, 446, 469, 478, 556, 566, 888, 899, 998,(The earliest I have ever found this term was in an article in the Bulletin of the California Mathematics Council in 1970. Does anyone know of an earlier usage?")
139 is the smallest factor of the 23rd Lucas number, It is the smallest Lucas number with prime index which is not prime itself.
139 is the sum of five consecutive primes, 19, 23, 29, 31, and 37.139 is the smallest factor of the smallest Lucas number to prime index, which is not prime.
139 and 149 are the first consecutive primes differing by 10 *Curious and Interesting Number by David Wells.
139 is the smallest prime for which the product of the digits is a prime cubed.
139 is the larger of a pair of twin primes.
If you take all the possible square pyramidal numbers, and subtract one, it seems that only three of these can ever be prime, 14-1, 30-1, and 140-1.
139 is the smallest prime that is the sum of six distinct squares. 1^2 + 2^2 + 3^2 + 5^2 + 10^2.
The 140th Day of the Year;
140 is the sum of the squares of the first seven positive integers. 12 + 22 + 32 + 42 + 52 + 62 + 72 = 140. *Prime Curios (and 7 is the largest prime factor of 140 And the 7 consecutive numbers starting with 140, all have an even number of prime factors, 140 is 2x2x5x7.
As the sum of the first seven consecutive squares, it is the 7th square pyramidal number. .
And how about an palindromic expression for 140, 2x5x7+7*5*2. from *@AmbigrammDesign
140 is a repdigit in bases 13 (aa), 19(7,7), 27(5,5), 34(4,4), 69(2,2), and 139(1,1).
140 is the fourth Harmonic divisor Number, the harmonic mean of its divisors. The harmonic mean is 12 divided by the sum of the reciprocals of the divisors (the 12 is because there are 12 of these divisors) \( \frac {12}{1/2 + 1/2 + 1/4 ...... 1/140} \) =5 All perfect numbers are Harmonic divisor numbers but the converse is not true. All Harmonic divisor numbers are Practical numbers, since some distinct subset of its proper divisors can be used to sum to any smaller number.
There are 140 x 1021 (140 followed by 21 zeroes) different configurations of the Rubik's Cube. *Cliff Pickover@pickover
140 is the magic constant of this 5x5 square by *Srinivasa Raghave K Can you see how to easily make one for day 135, or 145? Jeff Miller's Web site on the Earliest Use of Math Words says that Frenicle de Bessy used the term magic in the title to his book, Des quarrez ou tables magiques, published posthumously in 1693, twenty years after his death. The first use in English was the same year in "A New Historical Relation of the Kingdom of Siam." Appropriate to have de Bessey mentioned here, as he first noted the cubic relation of the Taxi-cab number, 1729 and Srinivasa is a big fan, I believe, of Ramanujan.
140 is the character limit on Twitter (or was)
A. J. Meyl proved in 1878 that only three tetrahedral numbers are also perfect squares,The largest of these is T(48) =1402 = 19600: T(1) = 1² = 1; T(2) = 2² = 4
There are 142 planer graphs with unlabeled vertices.A. J. Meyl proved in 1878 that only three tetrahedral numbers are also perfect squares,The largest of these is T(48) =1402 = 19600: T(1) = 1² = 1; T(2) = 2² = 4
140 is also a Harshad, or Joy-giver number, divisible by the sum of its digits.
A semi-magic knights tour is a knights tour in which the 64 numbers on the board are numbered, and the numbers the knight lands on in order are filled in along the rows of an 8x8 magic square grid. A semi-magic square is one where the rows and columns add up to the magic constant, but the diagonals do not. The first such square was produced by William Beverley in 1848. The first known true magic square was not achieved until 2003 by J C Meyriandgnac and G. Sternterbrink, who also showed that there are 140 different Semi-magic tours. *Number Freak, Derriek Nieberman.
The 141st Day of the Year:
The 141st day of the year; 141 is the first non-trivial palindrome appearing in the decimal expansion of Pi, appearing immediately after the decimal point, 3.14159. Tanya Khovanova, Number Gossip
141 is a palindrome in base ten, and also in base six (353)
141 is the second n to give a prime Cullen number (of the form n*2n + 1). Cullen numbers were first studied by Fr. James Cullen in 1905. (That prime is 393050634124102232869567034555427371542904833,) *David Wells, Curious and Interesting Numbers. 141 is the only Prime Cullen index below 1000. (strangly if you change the +1 to -1, you get lots of index numbers that produce primes, 2, 3, 6, 30... LOTS)
141 is the number of lattice paths from (0,0) to (6,6) using steps (2,0), (0,2), (1,1).
141 is the 31st Lucky Number. Lucky Numbers were introduced to the public in 1956 by Gardner, Lazurus, Metropolis and Ulam. They suggested naming the sieve that defines it as a Josephus Flavius sieve, because it resembled the counting out sieve in the Josephus problem from the 1st century. The sieve begins by counting out every second number and eliminating them (thus eliminating all the evens). Then counting again from the start, eliminate every nth number where n is the next number in the list after the first survivor. It should proceed something like this:
1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21...
1, 3, x, 7, 9, x, 13, 15, x, 19, 21, x
1, 3, 7, 9, 13, 15 x 21
Lucky searching to you all. Seems like a really good computer project for young programming students.
The 142nd Day of the Year:
there are 142 possible planar graphs with six vertices.
142 is the smallest Semi-prime (having exactly 2 prime factors), whose sum of divisors is a cube. 142+71+2+1 = 63
The binary representation of 142 has the same number of zeros and ones.
Using only the digits 1, 4, and 2, and a plus sign:
1+42+24+1 is a palindrome, and 1+4+1 is a palindrome, so
1 + 42 + 24 + 1 + 1 + 4+ 1 + 1 + 42 +24 + 1 is a palindrome, and equals 142.
142 is the number of ways of partitioning 25 into distinct parts... which must be the number of ways of partitioning them into odd parts according to Euler.
A pound is 453.59 grams. An ounce is 1/16 of that, or 28.349.. grams. A carat is .2 grams, so an ounce is about, but not quite, 142 carats. Number Freak, Derrick Nieberman
A semi-magic knights tour is a knights tour in which the 64 numbers on the board are numbered, and the numbers the knight lands on in order are filled in along the rows of an 8x8 magic square grid. A semi-magic square is one where the rows and columns add up to the magic constant, but the diagonals do not. The first such square was produced by William Beverley in 1848. The first known true magic square was not achieved until 2003 by J C Meyriandgnac and G. Sternterbrink, who also showed that there are 140 different Semi-magic tours. *Number Freak, Derriek Nieberman.
The 141st Day of the Year:
The 141st day of the year; 141 is the first non-trivial palindrome appearing in the decimal expansion of Pi, appearing immediately after the decimal point, 3.14159. Tanya Khovanova, Number Gossip
141 is a palindrome in base ten, and also in base six (353)
141 is the second n to give a prime Cullen number (of the form n*2n + 1). Cullen numbers were first studied by Fr. James Cullen in 1905. (That prime is 393050634124102232869567034555427371542904833,) *David Wells, Curious and Interesting Numbers. 141 is the only Prime Cullen index below 1000. (strangly if you change the +1 to -1, you get lots of index numbers that produce primes, 2, 3, 6, 30... LOTS)
141 is the number of lattice paths from (0,0) to (6,6) using steps (2,0), (0,2), (1,1).
141 is the 31st Lucky Number. Lucky Numbers were introduced to the public in 1956 by Gardner, Lazurus, Metropolis and Ulam. They suggested naming the sieve that defines it as a Josephus Flavius sieve, because it resembled the counting out sieve in the Josephus problem from the 1st century. The sieve begins by counting out every second number and eliminating them (thus eliminating all the evens). Then counting again from the start, eliminate every nth number where n is the next number in the list after the first survivor. It should proceed something like this:
1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21...
1, 3, x, 7, 9, x, 13, 15, x, 19, 21, x
1, 3, 7, 9, 13, 15 x 21
Lucky searching to you all. Seems like a really good computer project for young programming students.
\(141 \equiv 3 (\mod 6)\) and so 141 is expressible as the difference of two squares, using bases three apart. The two bases must sum to 141 / 3 = 47. So 22 and 25 should work, and 25² - 22² = 141
The 142nd Day of the Year:
there are 142 possible planar graphs with six vertices.
142 is the smallest Semi-prime (having exactly 2 prime factors), whose sum of divisors is a cube. 142+71+2+1 = 63
The binary representation of 142 has the same number of zeros and ones.
Using only the digits 1, 4, and 2, and a plus sign:
1+42+24+1 is a palindrome, and 1+4+1 is a palindrome, so
1 + 42 + 24 + 1 + 1 + 4+ 1 + 1 + 42 +24 + 1 is a palindrome, and equals 142.
142 is the number of ways of partitioning 25 into distinct parts... which must be the number of ways of partitioning them into odd parts according to Euler.
A pound is 453.59 grams. An ounce is 1/16 of that, or 28.349.. grams. A carat is .2 grams, so an ounce is about, but not quite, 142 carats. Number Freak, Derrick Nieberman
Bus 142 (the "Magic Bus"), whose number is clearly visible on the bus that Christopher McCandless lived in until his death in Alaska, features prominently on the bus in the film made about his life called Into the Wild
The 143rd Day of the Year
there are 143 three-digit primes.
Also, 143^2 is a divisor of 143143.HT to Matt McIrvin who found the pattern for numbers such that n^2 divides n.n (where the dot represents concatenation) and then found it is at OEIS I should point out that every number greater than one for which this is true involves the digits 143, in order, and includes a mystery offering from one-seventh.
143 is also the number of moves that it takes 11 frogs to swap places with 11 toads on a strip of 2(11) + 1 squares (or positions, or lily pads) where a move is a single slide or jump. This activity dates back to the 19th century, and the incredible recreational mathematician, Edouard Lucas *OEIS.
Prof. Singmasters Chronology of Recreational Mathematics suggests that this was first introduced in the American Agriculturalist in 1867, and I have an image of the puzzle below. The fact that they call it, "Spanish Game" suggests it has an older antecedent. (anyone know more?)
143 is the smallest composite number, n, such that 5^n + 2 is prime. (That's some big number) *Prime Curios
143 is the sum of seven consecutive primes, beginning with 11.
There is no decimal number n, such that n + (sum of its digits) = 143.
Waring's problem tells us that every number is the sum of at most 143 seventh powers.
\( 3^2 + 4^2 = 5^2 \) AND
\( 3^3+4^3+5^3=6^3 \)
BUT
\(3^4+4^4 + 5^4+6^4=7^4-143\) Another beautiful pattern, spoiled by an ugly truth!
143 is a repdigit in base 12 (BB) (that's eleven twelves plus eleven)
The 144th Day of the year.
144 is the largest possible SP (sum times product) number. If you take the sum of the digits of a number, and also the product of the digits, and then multiply the two outcomes, there are only three positive numbers for which you will get the original value. One works, trivially. The other two are 135 and 144. 135-> (1+3+5)*(1*3*5) = 9*15=135. 144->(1+4+4)*(1*4*4)= 9 * 16 = 144.
.A Good exercise for students is to take the SP product in a iteration to find out if it goes to zero, or repeats some pattern, or lands eventually on one of these three fixed points(that's four fixed points if you count zero). (Try it with your students). 23->5*6 = 30. 30-> 3*0 = 0.... fixed point.
144 is the only non-trivial square in the Fibonacci Sequence.In fact, there are only four Fibonacci numbers that are perfect powers, 0, 1, 8, and 144. And we haven't known that for so very long. Here is the story from , Professor Stewart's Incredible Numbers
In 1913 R. D. Carmichael proved his conjecture that for any Fibonacci Number F(n), greater than F(12)=144, has at least one prime factor that is not a factor of any earlier Fibonacci number.
\(144^5 = 27^5 + 84^5 + 110^5 + 133^5 \) This counter-example disproved Euler's Conjecture that n nth powers are needed to sum to an nth power. It is also part of one of the shortest papers ever published in a math journal(two sentences)
(Squares are important in knowing if a number, n is Fibonacci or not. N is Fibonacci IFF one or both of \(5n^2 \pm 4\) is a perfect square. )
144 is also the smallest square number which is also a square when its digits are reversed 144 = 12 2 while 441= 212
144 is the second smallest even square which has no prime for its two adjacent numbers, 143 = 11 x 13, 145 = 5 x 29 . There is only one more year after this which is a square with no adjacent prime.
The sum of the first 144 decimal digits of pi (don't use the 3.) is 666, "The Number of the Beast." One person wrote that they thought that was gross! ( sorryf :-{ , bad pun)
144 is the only year day that is a square number that is the perimeter of a primitive Pythagorean Triangle. (16, 63, 65) *Ben Vitale
Srinavas Raghava K gives four different expressions for 144 in different sets
Using the "golden ratio", \(\phi^2 + \phi^6 + \phi^10 + \phi^{-2} + \phi^{-6} + \phi^{-10} \)
With Trangular Numbers \( T_2 + T_8 + T_14 \)
With Lucas Numbers \( L_2 + L_ 6 + L_10\) students should observe the simmularity of the exponents with the golden ratio example.
With Fibonacci Numbers
\(F_12\) = 144
And from Das Ambigramm 144 = 2x2x3x3x2x2
1729, the famous Taxi-cab number, was known to Ramanujan because he was studying "Fermat near-misses", numbers where z^n was only one away from x^n + y^n for some x, y, z. In his case, 1729 was a cube that was one more than 9^3 + 10^3 = 1729, one more than 12^3. 144 is another such number, but seldom celebrated. 71^3 + 138^3 = 144^3 - 1. (there is one more smaller year day which also is a "Fermat near-miss" of this same kind, and it is related to 1729.)
And 144 appears in another cubic near-miss, 73^3 + 144^3 = 150^3 + 1
144 is the smallest Fibonacci number in a string of five consecutive Fibonacci numbers that sum to a prime number. It is also the 2nd smallest in another such sequence.
(and off the wall, did you ever notice if you take four consecutive Fibonacci numbers, A, B, C, D, then BC-AD = 1.)
144 is the largest magnitude for the determinant of a 9x9 binary matrix.
144 is the largest magnitude for the determinant of a 9x9 binary matrix.
And on a lighter side, another thought provoking cartoon from "Talking Numbers" by John Golden@mathhombre
144 has a special link with the numbers 17 and 12, which appear in Theon's ladder of approximations to the square root of two. 144 is the 17th triangular number, and the 12th square number. Every other number in Theon's ladder (even denominators) gives a list of ALL the numbers which are both square and triangular by their indices. 144 is the largest year day that is both triangular and square, the next such number is from the ratio 41/29 (the 41st triangular number and the 29th square number, 841.
The 145th Day of the Year: 145= 1! + 4! + 5!. There are only four such numbers in base ten. 1, 2 and 145 are three of them, what's the fourth? Such numbers are called factorions, a term created by Cliff Pickover in 1995
145 is the result of 34 + 43, making it a Leyland number. a number of the form xy + yx where x and y are integers greater than 1. They are named after the British number theorist, Paul Leyland. (There are ten days of the year that are Leyland numbers)
Prime Curios points out several curiosities related to 145, The 145th prime number is 829 and their concatenation, 145829 is prime. And the largest prime factor of 145, is 1+4+5+8+2+9. and 149 is congruent to 1 in mod 8, mod 2, and mod 9.
The process of summing the squares of the digits of a decimal number has two results, one is the eventual decent to 1, and being called a Happy number. 145 is the largest Unhappy number. Unhappy numbers eventually land on one of the numbers in the eight cycle, 4 → 16 → 37 → 58 → 89 → 145 → 42 → 20 → 4 ... (any three digit number, for example, produces a sum of squares less than or equal to 243. Any of the numbers you land on that are greater than 145 and less than 243 has a sum of squares of its digits that is less than itself, and eventually they land on one of the chains that lead to the eight cycle shown. Some numbers (like 99) iterate to a number greater than 145, but they then recede back into the inexorable "cycle of unhappiness" above. (A great exploration for students to create the trees of all numbers less than 200 that go to either 1, or the unhappy cycle)
The 145th Day of the Year: 145= 1! + 4! + 5!. There are only four such numbers in base ten. 1, 2 and 145 are three of them, what's the fourth? Such numbers are called factorions, a term created by Cliff Pickover in 1995
145 is the result of 34 + 43, making it a Leyland number. a number of the form xy + yx where x and y are integers greater than 1. They are named after the British number theorist, Paul Leyland. (There are ten days of the year that are Leyland numbers)
Prime Curios points out several curiosities related to 145, The 145th prime number is 829 and their concatenation, 145829 is prime. And the largest prime factor of 145, is 1+4+5+8+2+9. and 149 is congruent to 1 in mod 8, mod 2, and mod 9.
The process of summing the squares of the digits of a decimal number has two results, one is the eventual decent to 1, and being called a Happy number. 145 is the largest Unhappy number. Unhappy numbers eventually land on one of the numbers in the eight cycle, 4 → 16 → 37 → 58 → 89 → 145 → 42 → 20 → 4 ... (any three digit number, for example, produces a sum of squares less than or equal to 243. Any of the numbers you land on that are greater than 145 and less than 243 has a sum of squares of its digits that is less than itself, and eventually they land on one of the chains that lead to the eight cycle shown. Some numbers (like 99) iterate to a number greater than 145, but they then recede back into the inexorable "cycle of unhappiness" above. (A great exploration for students to create the trees of all numbers less than 200 that go to either 1, or the unhappy cycle)
The 145th prime number is 829, and 145829 is prime. Notice also, that the largest prime factor of 145 = 1+4+5+8+2+9, and that 145 is congruent to 1, mod 8, mod 2, and mod 9. *Prime Curios
145 is a palindrome in base 12, (101)
145 can be written as the sum of two squares in two different ways, 122+12 = 82+92
The 146th Day of the Year
146 is 222 in base eight. *What's So Special About This Number
Jim Wilder@wilderlab pointed out that the sum of the divisors of 146; 1+2+73+146 also equals 222. Finding value of 222 in base n is nice introduction to polynomials, and (IMHO) leads students to understand polynomials (and base 10) much better.
The decimal expansion of 1/293 has a period of 146 digits.
146 is a number n, for which n2+1 is prime. Goldbach conjectured that any number in this sequence could be written as the sum of two other numbers in the sequence. For 146, one such solution is 146 = 20 + 126 *OEIS
The absolute difference between any two digits of this number is prime. *Prime Curios, For how many three digit numbers is this true?
Another nice palindrome from Das Ambigram, 146 = 2x5x7+3+3+7x5x2
If you roll two pairs of standard fair dice, the number of ways that both pair can turn out with equal face value showing is 146 out of 1296. The numerator for getting any of the numbers 2 through 12, is an interesting sequence, 1 + 4 + 9 + 16 + 25 + 36 + 25 + 16 + 9 + 4 + 1.... Guess you could say all fair and SQUARE.
146 is Roman Numerals uses all the symbols below 1100, CXLVI once each.
The 147th Day of the Year
if you iterate the process of summing the cubes of the digits of a number starting with 147, you eventually start repeating 153. This seems to be true for all multiples of three.
Shorty palindrome from Das Ambigramm 147 = 7*3*7.
He also added that 147 = 4+5+6..... + 16 + 17 = 18+19+...+ 23+24.
144 is the sum of two Fibonacci numbers, F(12) + F(4 )= 144 + 3 = 147
The 146th Day of the Year
146 is 222 in base eight. *What's So Special About This Number
Jim Wilder@wilderlab pointed out that the sum of the divisors of 146; 1+2+73+146 also equals 222. Finding value of 222 in base n is nice introduction to polynomials, and (IMHO) leads students to understand polynomials (and base 10) much better.
The decimal expansion of 1/293 has a period of 146 digits.
146 is a number n, for which n2+1 is prime. Goldbach conjectured that any number in this sequence could be written as the sum of two other numbers in the sequence. For 146, one such solution is 146 = 20 + 126 *OEIS
The absolute difference between any two digits of this number is prime. *Prime Curios, For how many three digit numbers is this true?
Another nice palindrome from Das Ambigram, 146 = 2x5x7+3+3+7x5x2
If you roll two pairs of standard fair dice, the number of ways that both pair can turn out with equal face value showing is 146 out of 1296. The numerator for getting any of the numbers 2 through 12, is an interesting sequence, 1 + 4 + 9 + 16 + 25 + 36 + 25 + 16 + 9 + 4 + 1.... Guess you could say all fair and SQUARE.
146 is Roman Numerals uses all the symbols below 1100, CXLVI once each.
The 147th Day of the Year
if you iterate the process of summing the cubes of the digits of a number starting with 147, you eventually start repeating 153. This seems to be true for all multiples of three.
Shorty palindrome from Das Ambigramm 147 = 7*3*7.
He also added that 147 = 4+5+6..... + 16 + 17 = 18+19+...+ 23+24.
144 is the sum of two Fibonacci numbers, F(12) + F(4 )= 144 + 3 = 147
If there are no fouls, the maximum score on a snooker break is 147.
And Derek Orr@Derektionary pointed out that "147 is the smallest number formed by a column of numbers on a phone button pad"
147 in binary has an equal number of zeros and ones.
The binary form of 147 (10010011) contains all the two-digit binary numbers (00, 01, 10 and 11).
147 is a repdigit in base 20 (77), or 7 score and 7.
Not even sure if it is unusual, or how unusual, but 147 ends in a digit of three in bases 4, 6, 8, 9, 12, 16, and 36.
The 148th Day of the Year
148 is also a Loeschian number, a number of the form a2 + ab + b2. These numbers and the triples (a,b,L) formed by points in space are used, among other places in locations of spheres under hexagonal packing. (These numbers are named after August Loesch, German Economist {1906-1945})
A Vampire number is a number whose digits can be regrouped into two smaller numbers that multiply to make the original (1260 = 21*60). There are 148 vampire numbers with six digits. (There are 7 four-digit vampire numbers, which might be easier for younger students to find. (1260, 1395, 1435, 1530, 1827,and 2187)
148 is the 12th number in the Mian-Chowla sequence. The sequence starts with 1, and numbers are added in order if they do not a sum of some distinct collection of existing numbers. So 2 is in, and we have 1, 2. Now 3 can't be added since 1+2 = 3, so we go to four, .... 1,2,4. Now 5, 6, and 7 can all be formed from those present, so 8 will be next. (The sequence is named for Sarvadaman Chowla, a British born Indian American Mathematician (1907-1995, one of the co-creators.)
\(e^{\pi\sqrt{148}}\ is an integer..... almost, 39660184000219160.00096667...
And Derek Orr@Derektionary pointed out that "147 is the smallest number formed by a column of numbers on a phone button pad"
147 in binary has an equal number of zeros and ones.
The binary form of 147 (10010011) contains all the two-digit binary numbers (00, 01, 10 and 11).
147 is a repdigit in base 20 (77), or 7 score and 7.
Not even sure if it is unusual, or how unusual, but 147 ends in a digit of three in bases 4, 6, 8, 9, 12, 16, and 36.
The 148th Day of the Year
148 is also a Loeschian number, a number of the form a2 + ab + b2. These numbers and the triples (a,b,L) formed by points in space are used, among other places in locations of spheres under hexagonal packing. (These numbers are named after August Loesch, German Economist {1906-1945})
A Vampire number is a number whose digits can be regrouped into two smaller numbers that multiply to make the original (1260 = 21*60). There are 148 vampire numbers with six digits. (There are 7 four-digit vampire numbers, which might be easier for younger students to find. (1260, 1395, 1435, 1530, 1827,and 2187)
148 is the 12th number in the Mian-Chowla sequence. The sequence starts with 1, and numbers are added in order if they do not a sum of some distinct collection of existing numbers. So 2 is in, and we have 1, 2. Now 3 can't be added since 1+2 = 3, so we go to four, .... 1,2,4. Now 5, 6, and 7 can all be formed from those present, so 8 will be next. (The sequence is named for Sarvadaman Chowla, a British born Indian American Mathematician (1907-1995, one of the co-creators.)
\(e^{\pi\sqrt{148}}\ is an integer..... almost, 39660184000219160.00096667...
148 is a Palindrome in base 6(404) and base 36 (44).
The 149th Day of the Year
149 is the 35th prime number, and a twin prime with 151.
145 is an Emirp since 941, its reversal, is also a prime.
There are 149 ways to put 8 queens on a 7-by-7 chessboard so that each queen attacks exactly one other queen. *Prime Curios
149 in binary is 10010101. The zeros are in prime positions 2, 3, 5, and 7, when read left-to-right. These are the four single digit prime numbers.*Prime Curios
149 is a strictly non-palindromic number, it is not a palindrome in any base from 2 to 147.
149 is a full reptend prime, its reciprocal is 148 digits long, 1/149 repeats 0067114093959731543624161073825503355704697986577181208053691275167785234899328859060402684563758389261744966442953020134228187919463087248322147651 indefinitely.
also 149 = 62 + 72 + 82.(note that the digits 1, 4, 9 are squares also)
149 is also the sum of three primes, none of which are the sum of two squares, 23 + 43 + 83 And Derek Orr noted that the sum of the digits of 149, \(1 + 4 + 9 = 14 = 1^2 + 2^2 + 3^2 \)
149 is the smallest 3-digit prime with distinct digits in each position such that inserting a zero between any two digits creates a new prime (that is, 1049 & 1409 are both prime).
The 150th Day of the Year
150 is the largest gap between consecutive twin prime pairs less than a thousand. It occurs between {659, 661} and {809, 811}. *Prime Curios
2150 - 3 and 2150 - 5 are twin primes. BIG twin primes! and one more from Prime Curios.... 150 is the largest gap between consecutive twin prime pairs less than a thousand. It occurs between {659, 661} and {809, 811}.
150 is the sum of eight consecutive primes starting with 7.
150 is a Harshad(joy-giver) number, divisible by the sum of its digits.
A really nice sequence of infinite sums from Nakasu Wataru on Twitter,
\( \sum{k=1}^{\infty}(\frac{k}{2^k} = 2\)
\( \sum{k=1}^{\infty}(\frac{k^2}{2^k} = 6\)
\( \sum{k=1}^{\infty}(\frac{k^3}{2^k} = 26\)
\( \sum{k=1}^{\infty}(\frac{k^4}{2^k} = 150\)
And that's the last one that's a year day.
150 is a palindrome in base 4(2112), and in base 7(303) A Poly divisible number is an n-digit number so that for the first digit is divisible by one, the first two digits are divisible by two, the first three digits are divisible by three, etc up to n. There are 150 three-digit poly divisible numbers. Hat tip to Derek Orr .
150 = 5 x 2 x 5 + 5 x 2 x 5 + 5 x 2 x 5 HT to Das Ambigram
150 year celebration is called sesquicentennial of the event.
And... 150 is the number of degrees in the quincunx astrological aspect explored by Johannes Kepler.
Rubix Cube gotten too easy for you? Try the Professor's Cube, 150 movable facets.












No comments:
Post a Comment